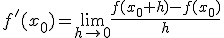Opracowanie:
Pochodne wzory
Pochodne wzory
Pochodna wzory-artykuł dla uczniów szkół średnich
Wielu osobom krew się mrozi na widok słowa pochodna, jednakże, nie jest ona taka straszna jak się wydaje. W tym artukule pokonam ten stereotyp i pokażę, że jest ona przyjemna do liczenia. Dowiesz się także jak obliczać pochodną funkcji za pomocą wzorów, rozwiążemy również sporo przykładów związanych z obliczaniem pochodnej funkcji oraz będziemy znajdować równanie prostej stycznej do wykresu funkcji.
1.Co już powinieneś/aś umieć aby zrozumieć ten artykuł?
-rozumieć pojęcie funkcji
-znać własności funkcji
-obliczać granicę funkcji
2.Zanim przejdziemy do obliczania pochodnej funkcji (w poniższym artykule pochodną będę oznaczał jako f'(x)-oznaczenie wprowadzone przez Lagrange’a, chociaż możemy się spotkać również z innymi oznaczeniami pochodnej funkcji) i jej zastosowania, powinniśmy najpierw zapoznać się z definicją pochodnej. Czy ta definicja będzie przydatna dla ucznia? Prawdopodobnie NIE-praktyczna część będzie dużo bardziej istotna. Aczkolwiek zapoznajmy się z definicją mimo wszystko:
Pochodna jest narzędziem matematycznym pozwalającym nam zmierzyć jak szybko funkcja rośnie (bądź maleje). Na samym początku zajmiemy się zrozumieniem wzoru pochodnej funkcji z definicji:
Wzór tylko sprawia pozory strasznego, jest on naprawdę prosty i przyjemny w użyciu! Wyprowadźmy sobie go:
Na osi OX zaznaczyłem punkt x0 oraz punkt x0+h (odległość punktu x0 od punktu x0+h jest równa oczywiście h). Następnie zaznaczyłem wartości jakie przyjmuje funkcja dla argumentów x0 i x0+h. Są to następująco f(x0) oraz f(x0+h). Ich różnica wynosi zatem f(x0+h)-f(x0). Przypomnijmy sobie teraz czym jest pochodna funkcji-jest to miara szybkości zmian wartości funkcji względem zmian jej argumentów. Zapiszmy to w innej postaci:
Taką postać nazywamy ilorazem różnicowym. Wyobraźmy sobie teraz, że przyrost argumentów jest bardzo bardzo bardzo mały, zatem zmiana wartości funkcji również będzie bardzo bardzo bardzo mała. Zapisując to matematycznie otrzymamy wzór na pochodną (zapisany powyżej) w punkcie x0. Gdybyśmy chcieli obliczyć pochodną funkcji (nie w punkcie, lecz ogólnie)zamiast x0 piszemy po prostu x.
Przykład 1: Oblicz pochodną funkcji f(x) w podanym punkcie x0:
a.) f(x)= -5x-1, x0=7
Rozwiązanie: Naszym celem jest obliczenie pochodnej funkcji w punkcie x0. Przed momentem poznaliśmy wzór na obliczenie pochodnej w punkcie. Wykorzystajmy go zatem, aby wykonać zadanie. Podstawiając pod wzór otrzymujemy granicę:
3. Do obliczenia pochodnej funkcji nie potrzebne jest liczenie granicy. Pochodną możemy obliczyć znając odpowiednie w wzory i własności pochodnej co ułatwia liczenie pochodnej w wielkim stopniu. Pochodne funkcji elementarnych-podstawowe wzory:
WZÓR 1: f(x)=c f'(x)= 0, gdzie c R
Przykład 2: f(x)=10 f'(x)= 0
WZÓR 2: f(x)= ax +b f'(x)= a
Przykład 3: f(x)=100x f'(x)=100
WZÓR 3: f(x)= xn f'(x)= nxn-1, gdzie x>0 i nR/{0,1}
Przykład 4: f(x)= x7 f'(x)= 7x6
WZÓR 4: f(x)= f'(x)= , gdzie x=/=0
Przykład 5: f(x)= f'(x)=
WZÓR 5: f(x)= f'(x)= , gdzie x>0
Przykład 6: f(x)= f'(x)=
4.Niektóre funkcje wyglądają odstraszająco, obliczenie takiej pochodnej jest znacznie bardziej monotonne i możliwość popełnienia błędu obliczeniowego jest dużo większa. Pomocne w takich sytuacjach jest znajomość podstawowych własności pochodnej funkcji
*Jeżeli funkcja f(x) jest złożona ze stałej (c) pomnożonej przez inną funkcję g(x) to wzór na obliczenie f'(x) ma następującą postać:
WZÓR 1: f(x)=c* g(x) f'(x)= c*g'(x)-iloczyn pochodnej przez stałą
*Jeżeli funkcja f(x) jest złożona z sumy dwóch funkcji g(x) i h(x) to wzór na obliczenie f'(x) ma następującą postać:
WZÓR 2: f(x)= g(x)+h(x) f'(x)=g'(x)+h'(x)-pochodna sumy funkcji
*Jeżeli funkcja f(x) jest złożona z różnicy dwóch funkcji g(x) i h(x) to wzór na obliczenie f'(x) ma następująca postać:
WZÓR 3: f(x)=g(x)-h(x) f'(x)=g'(x)-h'(x)-pochodna różnicy funkcji
*Jeżeli funkcja f(x) jest złożona z iloczynu dwóch funkcji g(x) i h(x) to wzór na obliczenie f'(x) ma następującą postać:
WZÓR 4: f(x)=g(x)*h(x) f'(x)=g'(x)h(x)+g(x)h'(x)-pochodna iloczynu funkcji
*Jeżeli funkcja f(x) jest złożona z ilorazu dwóch funkcji g(x) i h(x) to wzór na obliczenie f'(x) ma następującą postać:
WZÓR 5: f(x)= f'(x)= , gdzie h(x)=/=0- pochodna ilorazu funkcji
Przykład 7: Oblicz pochodną funkcji:
a.) f(x)= 3( )
Rozwiązanie: Możemy zauważyć, że funkcja f(x) składa się ze stałej c=3pomnożonej przez funkcję g(x)=. Użyjemy zatem wzoru 1 oraz wzoru 1 i 3 z podpunktu 3.
f'(x) = 3()’ = 3( ) =
Uwaga: WYMNOŻENIE STAŁEJ PRZEZ FUNKCJĘ g(x) NA SAMYM POCZĄTKU NIE JEST BŁĘDEM!
b.) f(x)=
Rozwiązanie: Zauważmy, że funkcja f(x) składa się z sumy i różnicy czterech różnych funkcji. Użyjemy zatem wzoru 1 i wzoru 2 jednocześnie z podpunktu 4 oraz wzorów 1 i 3 z podpunktu 3.
f'(x)=( )’= ()’ – ()’ + (10x)’ +7′ =
Uwaga: MOŻNA ODRAZU ZAPISAĆ WZÓR POCHODNEJ. NIE JEST WYMAGANE ROZPISANIE TEGO W SPOSÓB POKAZANY POWYŻEJ. ROZPISANIE TO MA NA CELU POKAZAĆ ODBIORCY TEGO ARTYKUŁU W JAKI SPOSÓB POCHODNA ZOSTAŁA OBLICZONA ;). W PODPUNKCIE C ZAPIS TEN JEST JUŻ POMINONY.
c.) f(x)=
Rozwiązanie: Zauważmy, że funkcja f(x) jest złożona z iloczynu dwóch funkcji g(x)=x-1 oraz h(x)=x2+x+1. Użyjemy zatem wzoru 4 z podpunktu 4 oraz wzoru 1 i 3 z podpunktu 3.
f'(x)=(x-1)'(x2+x+1) + (x-1)(x2+x+1)’ = 1(x2+x+1) + (x-1)(2x+1)= x2+x+1+2x2+x-2x-1=3x2
Uwaga: JEŻELI NADAL MASZ PROBLEMY Z OBLICZANIEM POCHODNEJ ROZPISZ f'(x) na f'(x)=(x-1)'(x2+x+1) + (x-1)(x2+x+1)’ =[(x)’-1′](x2+x+1) + (x-1)[(x2)’+(x)’+1′]. WYMNOŻENIE FUNKCJI g(x) i h(x) I NASTĘPNIE OBLICZENIE POCHODNEJ FUNKCJI f(x) ZA POMOCĄ WZORÓW Z PODPUNKTU 4 RÓWNIEŻ JEST POPRAWNYM ROZWIĄZANIEM.
d.) f(x)=
Rozwiązanie: Możemy zauważyć, że funkcja f(x) jest złożona z ilorazu dwóch funkcji g(x)=x2+3 oraz h(x)=x2+4. Użyjemy zatem wzoru 5 z podpunktu 4 oraz wzorów 1 i 3 z podpunktu 3.
f'(x)= = =
Uwaga: JAK MOŻNA ZAUWAŻYĆ NIE UPRASZCZAŁEM MIANOWNIKA FUNKCJI. DLACZEGO? JAK SIĘ OKAŻĘ NIE BĘDZIĘ TO POTRZEBNE W ZADANIACH, W KTÓRYCH WYMAGANE BĘDZIE OBLICZENIE POCHODNEJ FUNKCJI NP. ZADANIACH OPTYMALIZACYJNYCH CZY ZBADANIU MONOTONICZNOŚCI FUNKCJI
5.Aby wyćwiczyć i zamknąć temat obliczania pochodnej funkcji obliczmy kilka pochodnych dla treningu.
zykład 1: Oblicz pochodną funkcji
Przykład 8: Oblicz pochodną funkcji:
a.) f(x)= x6 – 2x4
Rozwiązanie: Zauważmy, że funkcja f(x) złożona jest z różnicy dwóch funkcji elementarnych, zatem :
f'(x)= 6 x5-2 4x3= 3x5-8x3
b.) f(x)=x2( +x)
Rozwiązanie: Najpierw wyznaczmy dziedzinę funkcji f(x). Dziedziną tej funkcji będzie x>0 . Następnie zauważmy, że funkcja f(x) jest złożona z iloczynu dwóch funkcji, oznaczmy je jako g(x) i h(x). Gdzie g(x)=x2 oraz h(x)= +x. Zastosujmy zatem wzór na pochodną iloczynu funkcji. Przypomnijmy go sobie: f'(x)=g'(x)h(x)+g(x)h'(x), zatem:
f'(x)=2x( +x) + x2( + 1) = 2x + 2x2 – + x2 = 3x3 + 2x – = 3x2 + x
c.) f(x)=
Rozwiązanie: Na samym początku zacznijmy od wyznaczenia dziedziny funkcji. Wiemy, że mianownik nie może być równy 0, zatem:
x3-1=/=0
(x-1)(x2+x+1)=/=0
x=/=1
Dziedziną funkcji jest zatem zbiór liczb rzeczywistych z wyrzuceniem 1- D=x R{1}
Zauważmy, że funkcja f(x) składa się z ilorazu dwóch funkcji. Oznaczmy je jako g(x) i h(x). Gdzie g(x)=x2+x-1 oraz h(x)= x3-1, zatem:
f'(x)= = =
6.Ostatnim wzorem wymaganym od maturzystów oraz uczniów szkół średnich jest a=f'(x0)
Gdzie f'(x0) w tym przypadku jest pochodną funkcji w punkcie x0 i jest ona równa współczynnikowi kierunkowemu (a) prostej (funkcji o równaniu ogólnym y=ax+b). Dzięki temu wzorowi możemy wyznaczyć równanie stycznej do wykresu funkcji f(x). Wszystko się rozjaśni gdy przerobimy kilka przykładów. Zaczynajmy!
Przykład 9: Oblicz współczynnik kierunkowy a stycznej do wykresu funkcji f w punkcie x0, gdy:
a.) f(x)= x2+x-1 i x0=1
Rozwiązanie: Aby wyznaczyć pochodną funkcji w punkcie x0 musimy najpierw obliczyć pochodną funkcji f(x). Zauważmy, że składa się ona z sumy 3 funkcji elementarnych. Użyjemy zatem wzoru na pochodną sumy funkcji oraz wzorów z podpunktu 3.
f'(x)=2x+1
Następnym etapem rozwiązania jest podstawienie punktu x0=1 pod pochodną funkcji f(x).
f'(1)= 2 + 1 = 3
Zgodnie ze wzorem a=f'(x0), możemy wywnioskować, że współczynnik kierunkowy prostej stycznej do wykresu funkcji f(x) wynosi 3.
Uwaga: Możemy obliczyć pochodną funkcji za pomocą wzoru opisanego w podpunkcie 2, aczkolwiek jest on mało praktyczny i dużo łatwiej oblicza się pochodną funkcji używając wzorów z podpunktów 3 i 4.
b.) f(x)= i x0=4
Rozwiązanie: Najpierw wyznaczamy dziedzinę funkcji, następnie obliczamy pochodną funkcji, a na z=sam koniec podstawiamy punkt x0=4 pod otrzymany wzór pochodnej funkcji. Otrzymany wynik będzie naszym współczynnikiem kierunkowym a stycznej do wykresu funkcji w punkcie x0
D=x R{0}
f'(x)=(x + )’= –
f'(4)= – = – =0 a=0
Przykład 10: Funkcja f określona jest wzorem f(x)= dla x==0. Prosta o równaniu x=-2 przecina wykres funkcji f w punkcie P. Znajdź równanie stycznej do wykresu funkcji w punkcie P.
Rozwiązanie: W zadaniu nie mamy podanego punktu styczności funkcji f oraz prostej stycznej do funkcji f. Tym samym nie jesteśmy obliczyć od razu współczynnika kierunkowego stycznej (a), nie możemy również wyliczyć wyrazu wolnego (b) prostej y=ax+b. Jeżeli jednak znajdziemy współrzędne punktu P, będziemy mogli obliczyć obie niewiadome (a i b).
krok 1: Obliczam współrzędne punktu P.
Jeżeli prosta x=-2 przecina wykres funkcji w punkcie P możemy wywnioskować, że pierwsza współrzędna punktu P będzie równa x0=-2. Możemy zatem teraz obliczyć drugą współrzędną tego punku podstawiając x=-2 pod wzór funkcji f(x):
y0= = 8 P(-2 ; 8)
krok 2: Obliczam pochodną funkcji f(x)
f'(x)= =
krok 3: Obliczam pochodną funkcji w punkcie x0=-2
f'(-2)=-4 a=-4
krok 4: Obliczam wyraz wolny (b) stycznej y=ax+b do wykresu funkcji f(x)
y=ax+b
y=-4x+b
Wiemy, że punkt P spełnia równanie prostej f, ale także spełnia on równanie stycznej do wykresu funkcji f, zatem możemy wyliczyć wyraz wolny stycznej
8=8+b
b=0 y=-4x
Odpowiedź: Równanie prostej stycznej do wykresu funkcji f ma postać y=-4x
Bibliografia: Powyższe zadania wybrałem z książek ,,Matura z Matematyki 2018-… poziom rozszerzony i podstawowy”, autorstwa Andrzeja Kiełbasy oraz Piotra Łukasiewicza oraz ,,Zbiór zadań maturalnych-zakres rozszerzony” wydawnictwa Podkowa