Ośmiokąt foremny

Ośmiokąt (inaczej oktagon, ośmiobok) foremny – figura geometryczna o ośmiu bokach tej samej długości i ośmiu kątach wewnętrznych tej samej miary.

Miara kątów wewnętrznych.
Do określenia miary kątów wewnętrznych ośmiokąta foremnego potrzebny będzie nam wzór na miarę kąta wewnętrznego w wielokącie foremnym. Jest on bardzo prosty do wyprowadzenia. Ponieważ każdy wielokąt foremny można podzielić na n trójkątów (w przypadku ośmiokąta n będzie równe osiem, ponieważ ma on osiem boków będących podstawą każdego z tych trójkątów), a suma kątów w trójkącie wynosi 180°, możemy stwierdzić, że szukany wzór będzie wyglądał następująco:

gdzie:
α- miara kąta wewnętrznego wieloboku
n- liczba kątów wewnętrznych wieloboku
Krótkie podsumowanie wzoru: miara kąta wewnętrznego równa jest sumą miar kątów wszystkich trójkątów równoramiennych składowych na dany wielokąt zmniejszoną o sumę miar kątów między ramionami tych trójkątów (tworzą one kąt pełny, stąd 360°) dzieloną przez liczbę kątów wielokąta. Po wyciągnięciu przed nawias 180° uzyskujemy drugie równanie.

Po wyliczeniu więc z tego wzoru, wiemy że α dla ośmiokąta foremnego jest równa 135°.

Suma miar kątów wewnętrznych ośmiokąta foremnego to 1080°.
Dodatkowo, dzięki temu, że wyprowadziliśmy wzór zależny od ilości boków w wielokącie, jest on uniwersalny i można go zastosować w liczeniu miary kątów wewnętrznych w każdym wielokącie foremnym.

2. Twierdzenie.
Na każdym wielokącie foremnym można opisać okrąg i w każdy wielokąt foremny można wpisać okrąg.

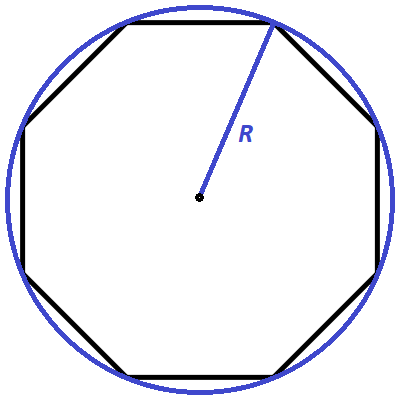
Wzór na promień okręgu opisanego na ośmiokącie foremnym:

gdzie:
R- długość promienia okręgu opisanego na ośmiokącie
a- długość boku ośmiokąta

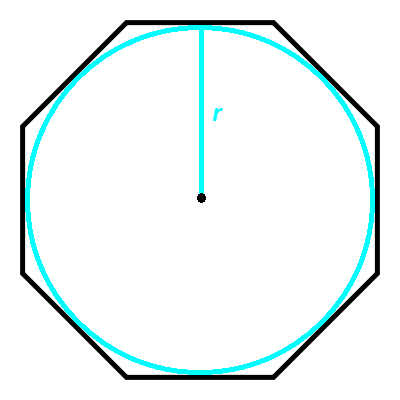
Wzór na promień okręgu wpisanego w ośmiokąt foremny to:

gdzie:
a- długość boku ośmiokąta
r- długość promienia okręgu wpisanego w ośmiokąt foremny

Przykładowe rozwiązanie: dla a= 5cm



źródło plików (zdjęć) w tym punkcie: https://calcoolator.pl/obwod-pole-przekatne-wysokosc-osmiokata.html

3. Obwód.
Prawdopodobnie bez większego zaskoczenia, obwód ośmiokąta foremnego równy jest sumie miar jego boków.


gdzie:
L- obwód
a- długość boku wielokąta

4. Pole powierzchni.
Wzór na pole powierzchni ośmiokąta foremnego to:

gdzie:
S- pole ośmiokąta
a- długość boku ośmiokąta.
Do wyprowadzenia wzoru wykorzystywane jest twierdzenie (o okręgach opisanych w wielokącie foremnym i na wielokącie foremnym) opisane w punkcie 2 i twierdzenie cosinusów dla trójkąta równoramiennego o bokach R, R, a (gdzie R- promień okręgu opisanego na wielokącie foremnym).

Przykładowe rozwiązanie: dla a= 9cm

5. Wysokość.
Do wyprowadzenia wzoru na wysokość ośmiokąta foremnego, znowu skorzystamy z twierdzenia opisanego w punkcie 2 i ze wzoru na promień okręgu wpisanego w ten ośmiokąt. Ponieważ okrąg wpisany w ośmiokąt foremny jest styczny z każdym bokiem tego ośmiokąta, dokładnie w połowie każdego z tych boków, oznacza to, że średnica (którą można zapisać jako dwa promienie) tego okręgu jest równa wysokości ośmiokąta. Więc:

gdzie:
h- wysokość ośmiokąta foremnego
a- długość boku ośmiokąta
r- promień okręgu wpisanego w ośmiokąt

6.Przekątne.
Ośmiokąt foremny ma trzy rodzaje przekątnych:
-najdłuższa przekątna (w ilości 4) – odcinek od jednego wierzchołka ośmiokąta do przeciwległego mu wierzchołka. Wzór:

-przekątna średniej długości (w ilości 8) – odcinek prostopadły do dwóch przeciwległych boków, jest jednocześnie wysokością ośmiokąta. Wzór:

-przekątna najkrótsza (ilość – 8) – odcinek od jednego wierzchołka ośmiokąta do drugiego najbliższego mu wierzchołka (tj. wierzchołka mu najbliższego z pominięciem wierzchołka koło niego). Wzór:

legenda do wszystkich wzorów w tym punkcie:
P1 – długość najdłuższej przekątnej ośmiokąta
P2 – długość przekątnej średniej długości
P3 -długość najkrótszej przekątnej ośmiokąta
a- długość boku ośmiokąta
h- wysokość ośmiokąta