Opracowanie:
Definicja funkcji trygonometrycznych
Definicja funkcji trygonometrycznych
Funkcji trygonometrycznych w trójkącie prostokątnym wyróżniamy cztery.
Zacznijmy od przypomnienia tych funkcji. Zacznijmy od sinusa. Skrót tej funkcji trygonometrycznej to „sin”.
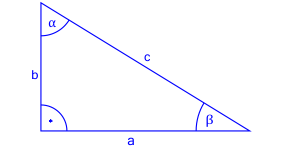
Zgodnie z powyższym rysunkiem napiszmy wzór i definicję sinusa.
Sinus kąta ostrego w trójkącie prostokątnym to stosunek przyprostokątnej leżącej naprzeciwko tego kąta do przeciwprostokątnej. Istotna jest kolejność stosunku tych długości.
W takim razie
Przejdźmy do cosinusa. Skrót „cos”
Cosinus kąta ostrego w trójkącie prostokątnym to stosunek przyprostokątnej leżącej przy kącie do przeciwprostokątnej.
Następnie mamy dwie funkcje trygonometryczne, do których nie potrzebujemy długości przeciwprostokątnej.
Jest to tangens i cotangens.
Zacznijmy od tangensa („tg”)
Jest to stosunek przyprostokątnej leżącej na przeciwko kąta do przyprostokątnej leżącej przy kącie.
Następnie przejdźmy do cotangensa. („ctg”)
Cotangens to stosunek przyprostokątnej leżącej przy kącie do przyprostokątnej leżącej naprzeciwko kąta. Cotangens jest odwrotnością tangensa.
Spróbujmy obliczyć wartości funkcji trygonometrycznych na konkretnych liczbach
Oblicz wartości funkcji trygonometrycznych trójkąta poniżej. Wiedząc, że przyprostokątne mają długość 8 i 6.
Ustalmy, że a=8; b=6.
Obliczmy przeciwprostokątną z twierdzenia Pitagorasa.
Podstawiając
82+62=c2
64+36=c2
c2=100
c= 10
Skoro mamy podane wszystkie boki, możemy zabrać się do obliczania wartości funkcji trygonometrycznych.
Funkcje trygonometryczne mamy już obliczone dla kąta .
Obliczmy teraz dla kąta .