Odległość punktów

Najkrótszą odległością punktu od prostej jest odcinek od danego punktu do punktu na prostej położony pod kątem prostym. Można ją obliczyć ze wzoru: .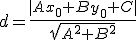
Współliniowość oznacza, że punkty są współliniowe gdy należą do tej samej jednej prostej. Odległość dwóch punktów oznacza się w sposób |AB|. O odległości punktów mówimy wtedy, gdy AB jest liczbą nieujemną, a |AB| jest zerem tylko, jeśli A=B oraz, gdy trzy punkty A, B i C są współliniowe, to: |AB| + |BC| = |AC|, |AB| + |AC| = |BC| lub |BC| + |AC| = |AB|, albo, gdy te trzy punkty nie są współliniowe, to (podobnie jak zasada, by można było narysować trójkąt, czyli suma dwóch krótszych boków musi być większa od najdłuższego boku): |AB| + |BC| > |AC| i |BC| + |CA| > |BA| i |CA| + |AB| > |CB|.
Zawsze odległość od punktu A do punktu B w linii prostej jest to najkrótsza odległość między tymi punktami. Zawsze odległość od punktu A do punktu B jest taka sama jak odległość od punktu B do punktu A.
Odległość między punktami ( , ) i ( , ) można obliczy ze wzoru: .