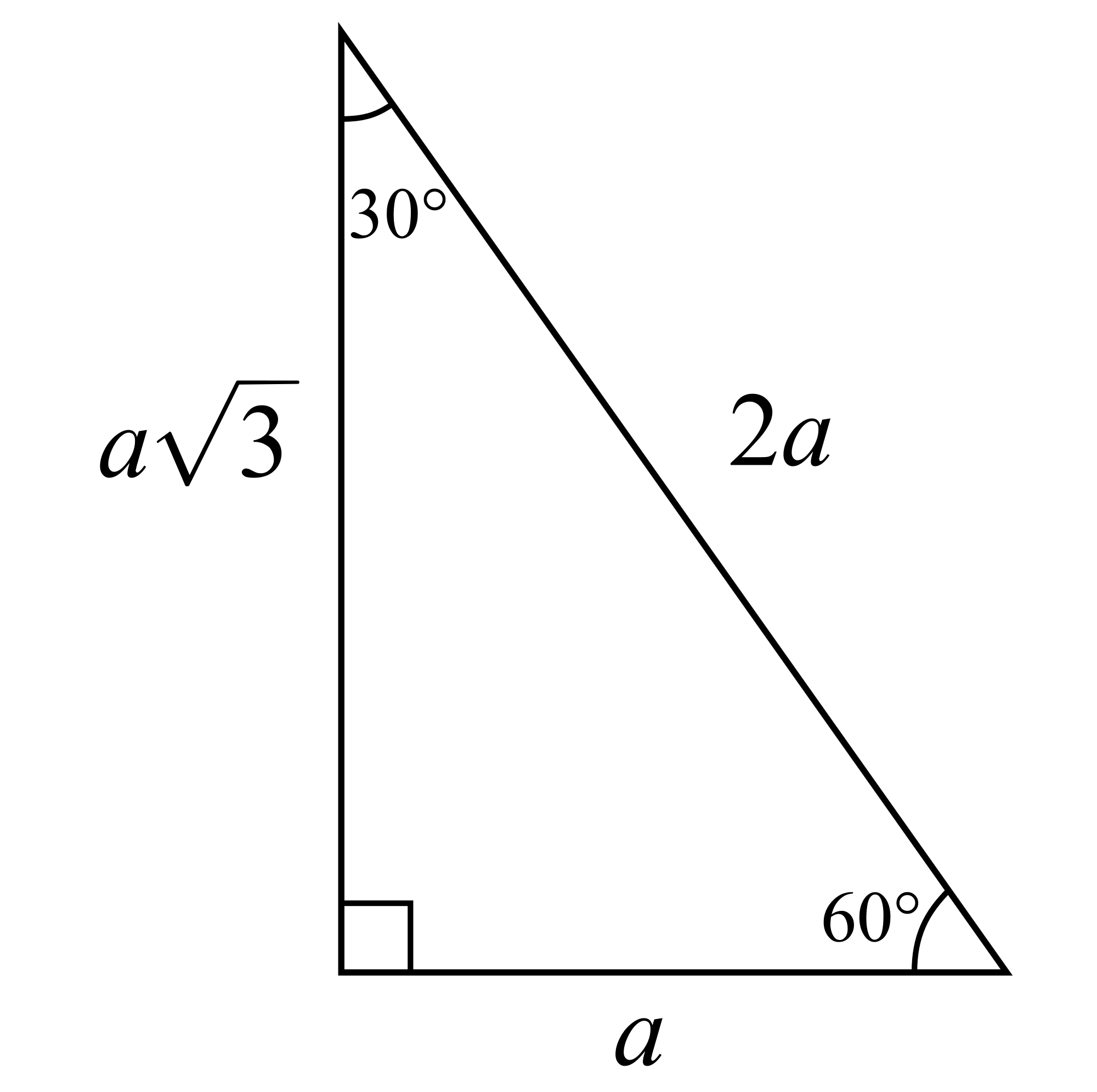
Trójkąt 30 60 90

Trójkąt 300,600,900 jest charakterystycznym trójkątem. Znamy zależności między jego bokami, które Wam przedstawię:
Naprzeciwko kąta 900 (największego kąta w tym trójkącie) mamy bok „2a”
Naprzeciwko kąta 600 (średniego kąta w tym trójkącie) mamy bok „ „
Naprzeciwko kąta 300(najmniejszego kąta w tym trójkącie) mamy bok „a”
Sprawdźmy za pomocą Twierdzenia Pitagorasa czy faktycznie jest to prawda.

Twierdzenie Pitagorasa: a2+b2=c2
Podstawmy zatem za a i b przyprostokątne, natomiast za c przeciwprostokątną.

Obliczmy lewą stronę równania:


Teraz obliczmy prawą stronę równania:


Strona prawa jest równa lewej, w takim razie zależności między bokami są prawdziwe.
Żeby łatwiej zapamiętać naprzeciwko którego kąta jest jaki bok wystarczy zapamiętać:
Naprzeciwko największego kąta najdłuższy bok (kąt 900, bok 2a)
Naprzeciwko średniego kąta średni bok (kąt 600, bok a
Naprzeciwko najmniejszego kąta najkrótszy bok (kąt 300, bok a)
Znając te zależności przećwiczmy je na przykładach.

Zacznijmy od podpunktu a
a) Naprzeciwko kąta 300 mamy bok równy 2
Korzystając z tego, że naprzeciwko najmniejszego kąta mamy najkrótszy bok. Wiemy że a=2. Obliczmy w takim razie 2a, czyli bok leżący naprzeciwko kąta prostego. Na naszym rysunku oznaczenie tego boku to a. Ma on długość 2*2, czyli 4. Pozostały bok b, to ten, który leży naprzeciwko kąta 600,czyli ma on postać a, w naszym przypadku 2 .
Zgodnie z rysunkiem
a=4
b= 2
Przejdźmy do kolejnego trójkąta
Naprzeciwko kąta 900 mamy bok równy 5.
Naprzeciwko największego kąta- najdłuższy bok (2a).
5=2a
a=2,5
„a” to bok leżący naprzeciwko kąta o mierze 300.
W takim razie zgodnie z naszym rysunkiem c=2,5.
Pozostało nam do obliczenia d.
Jest to bok, który leży naprzeciwko kąta 600, czyli ma postać a. Zgodnie z naszymi obliczeniami 2,5 .
c=2,5
d=2,5
Przejdźmy do następnego trójkąta
Mamy podany bok 6 i jest on położony naprzeciwko kąta 600.
a =6
a=6
„a” to bok położony naprzeciwko kąta 300, w naszym przypadku na rysunku bok oznaczony literką e.
Został nam bok, który jest naprzeciw kąta 900. Ma on postać 2a.
Jeżeli a=6
to 2a=12
Czyli bok f=12
Podsumowując
e=6
f=12
Zabierzmy się za następny trójkąt.
Naprzeciwko kąta 300 mamy bok o długości 3, czyli „a”.
Bok naprzeciwko 900 ma postać 2a, czyli 6. Na naszym rysunku jest to bok oznaczony literką g.
Został nam bok naprzeciwko kąta 600. Ma on postać a.
Jeżeli a=3, to bok naprzeciwko tego kąta jest równy .
W takim razie
g=6
h=3
b) W tym trójkącie mamy podany bok naprzeciwko kąta 900. Jest on równy 7, a jego postać to 2a.
Jeżeli 2a= 7
a=3,5
„a” to bok leżący naprzeciwko 300, czyli na naszym rysunku oznaczony literką a.
Pozostał nam bok naprzeciwko kąta 600. Ma on postać a . W naszym przypadku jest oznaczony literą b i ma wartość .
a=3,5
b=3,5
Przejdźmy do trójkąta obok. Naprzeciwko kąta 300 mamy bok długości 4.
Oznacza to, że a=4.
Bok naprzeciwko kąta 900 ma postać 2a, czyli 8. Na naszym rysunku jest to bok oznaczony literką c.
Naprzeciwko kąta 600 bok jest oznaczony literą d i ma postać a, czyli 4.
c=8
d=4
W następnym trójkącie mamy podany bok, który jest położony naprzeciwko kąta 900, który ma postać 2a.
Na naszym rysunku jest równy 8, co oznacza że a, czyli bok leżący naprzeciwko kąta 300 ma wartość 4. (bok oznaczony literą f). Pozostał nam bok oznaczony jako „e”, który ma postać a. W naszym przypadku 4.
e=4
f=4
Pozostał nam ostatni trójkąt w, którym mamy podany bok naprzeciwko kąta 600. Wiemy, że ma on postać a.
Na naszym rysunku ma wartość , co znaczy, że a (bok położony naprzeciwko kąta 300) ma wartość 1.
Bok 2a, ten który leży naprzeciwko kąta 900, ma wartość 2.
g=1
h=2

Obliczmy zatem długość x, a następnie y.
Mamy podaną przyprostokątną leżącą naprzeciwko kąta 600, ma ona długość 4.
Wiemy, że naprzeciwko kąta 600 bok ma postać a .
Wynika więc z tego, że 4=a .
Wyliczmy z tego równania a:
a
Podzielmy obie strony równania przez
a=
Wyłączmy niewymierność z mianownika mnożąc razy
a=
Wyznaczyliśmy długość boku, który ma postać „a”. Jest to bok, który leży naprzeciwko kąta 300.
Na naszym rysunku jest to bok oznaczony jako „y”.
y=
Bok oznaczony na naszym rysunku literką „x” jest to bok położony naprzeciwko kąta o mierze 900, czyli ma postać 2a.
Jeżeli obliczyliśmy, że a wynosi , możemy wyznaczyć ile będzie miał bok o długości 2a.
a=
Pomnóżmy razy 2, żeby otrzymać bok 2a.

Wyznaczyliśmy, że :
x=
y=
Zależności między bokami mamy już przećwiczone.

Z trójkąta prostokątnego możemy wyznaczyć stałe wartości funkcji trygonometrycznych.

Przypomnijmy czym jest sinus, cosinus, tangens i cotangens.
Sinus jest to stosunek przyprostokątnej leżącej naprzeciwko kąta do przeciwprostokątnej. (sin)
Cosinus jest stosunkiem przyprostokątnej leżącej przy kącie do przeciw prostokątnej. (cos)
Tangens to stosunek przyprostokątnej leżącej naprzeciwko kąta do przyprostokątnej leżącej przy kącie (tg)
Cotangens to odwrotność tangensa. Stosunek przyprostokątnej leżącej przy kącie do przyprostokątnej leżącej naprzeciwko kąta.
Obliczmy zatem wartości funkcji trygonometrycznych.








Zróbmy przykładowe zadanie korzystając z wartości funkcji trygonometrycznych, które przed chwilą wyznaczyliśmy.
Zadanie 1

Oblicz wysokość rombu.
Jak wiemy wysokość skierowana jest na bok pod kątem prostym.
Mamy więc trójkąt 30,60,90.
Naprzeciwko 900, mamy bok równy 6. Jest to 2a.
W takim razie bok a, naprzeciwko kąta 300 ma długość 3. Wysokość jest to bok położony naprzeciwko kąta 600, więc ma postać a .
W naszym wypadku a jest równe 3. Czyli wysokość ma długość 3 .
h=3
Zadanie 2
Oblicz pole trójkąta, który ma kąt prosty przy wierzchołku C, a wysokość poprowadzona z tego wierzchołka opada na bok AB łącząc się z punktem D położonym na tym boku.

Zacznijmy od przypomnienia wzoru na pole trójkąta. , z czego „a” to podstawa, a „h” to wysokość.
Nie mamy podanej podstawy ani wysokości.
Wiemy jednak, że kąt ACB ma 900, kąt ABC ma 300 i kąt BAC jest dorównaniem do 1800 czyli ma 600.
Wypiszmy co mamy podane.
CD= wysokość (h)
CB= 6cm
Kąt ADC= 900
Kąt ACB= 900
Kąt ABC= 300
Kąt BDC= 900
Kąt BAC= 600.
Wysokość podzieliła nam trójkąt ABC na dwa trójkąty. Trójkąt BCD oraz trójkąt ACD.
Zacznijmy od trójkąta CBD.
Bok CB o długości 6cm leży naprzeciwko kąta 900,czyli ma postać 2a.
Obliczmy zatem a, czyli długość boku który leży naprzeciwko kąta 300. W naszym przypadku jest to wysokość (h).
2a=6cm
a=3cm
Wysokość ma długość 3cm.
Brakuje nam jeszcze długość boku AB.
Patrzymy teraz na cały duży trójkąt ABC.
Bok CB o długości 6cm, jest położony naprzeciwko kąta BAC= 600. Wyliczmy zatem bok, który leży naprzeciw kąta 300 i ma postać „a”.
Naprzeciwko kąta 600 położony jest bok a .
a =6
Podzielmy obie strony równania przez , żeby otrzymać a.
a=
Wyłączmy niewymierność z mianownika mnożąc razy
a=
Skróćmy ułamek.
acm
Musimy obliczyć długość boku AB, który jest położony naprzeciwko kąta o mierze 900.
Ma on postać 2a.
AB= cm
AB=cm
Mamy podaną podstawę oraz wysokość, zatem możemy obliczyć pole trójkąta ABC.
Podstawa= cm
Wysokość=
Pole trójkąta
P=
P=
P=
Zadanie 2
Dany jest trójkąt prostokątny ABC, w którym kąt ACB= 900, natomiast kąt ABC=600. Niech D będzie punktem wspólnym wysokości poprowadzonej z wierzchołka C kąta prostego i przeciwprostokątnej AB tego trójkąta. Wykaż, że odcinek AD jest trzy razy dłuższy od odcinka DB

Z obrazka można zauważyć, że kąt ACB ma miarę 900.
Pozostałe kąty mają miarę 300 oraz 600, co oznacza, że stykamy się z trójkątem charakterystycznym 30,60,90.
Wysokość h poprowadzona z wierzchołka C podzieliła nam trójkąt na dwa mniejsze, również charakterystyczne 30,60,90. Przypomnijmy, że suma miar kątów w trójkącie jest równa 1800, w takim razie kąt BCD ma miarę 300, natomiast kąt DCA, ma miarę 600.
Zacznijmy od trójkąta ADC i obliczmy długość odcinka AD (x).
Skorzystajmy z faktu, że tg 300=
Podstawiając:
tg 300=

Pomnóżmy razy x

Następnie podzielmy przez
x=
x=

Obliczmy y
Skorzystajmy z tangensa600.
Wiemy, że tg 600=
Przypomnijmy definicję tangensa.
Tangens (tg), jest to stosunek przyprostokątnej leżącej naprzeciwko kąta do przyprostokątnej leżącej przy tym kącie.
W naszym przypadku tangens 600=
Podstawmy za tangens

Pomnóżmy obustronnie razy y.
Otrzymujemy:

Żeby obliczyć y musimy podzielić obie strony równania przez .

Wyłączmy niewymierność z mianownika (mnożymy razy ).
y=
Wniosek:
Jeżeli y= , natomiast x=, to x jest trzy razy większy od y.
C.N.D.

Zbierzmy zatem na koniec wszystkie informacje o trójkątach prostokątnych 30,60,90
Trójkąt 30,60,90 jest charakterystycznym trójkątem, w którym znamy wartości boków.
Naprzeciwko kąta 90 stopni położony jest bok, którego długość jest równa „2a”.
Naprzeciwko kąta 60 stopni położony jest bok, o długości „a„
Naprzeciwko kąta 30 stopni położony jest bok, którego długość wynosi „a”
Zależności między bokami a kątami w trójkątach 30,60,90:
Naprzeciwko największego kąta (90) najdłuższy bok(2a)
Naprzeciwko średniego kąta (60) średni bok (a)
Naprzeciwko najmniejszego kąta (30) najkrótszy bok (a)
Wartości funkcji trygonometrycznych kątów w trójkącie 30,60,90:
sin 300=
cos 300=
tg 300=
ctg 300=

sin 600=
cos 600=
tg 600=
ctg 600=

Myślę, że wszystkie te informacje, które tu umieściłam będą dla was przydatne.
Miłej nauki!