Opracowanie:
Graniastosłup
Graniastosłup
Na początku zacznijmy od tego czym jest graniastosłup.
Graniastosłup jest figura przestrzenna [czyli figura posiadająca nie tylko długość i szerokość (czyli boki figury) lecz także wysokość, która nie jest umiejscowiona na boku figury, za chwilę zobaczysz jak wyglądają], która posiada:
-dwie podstawy (są dwa przystające oraz równolegle wielokąty)
-ściany boczne (są najczęściej prostokątami, a ich ilość zależy od wielokąta w podstawie)
Graniastosłupy dzielimy na dwie grupy (ze względu na ułożenie ścian bocznych):
a) graniastosłupy proste: w tym rodzaju graniastosłupów ściany boczne (będące wyłącznie prostokątami) są ułożone pod kątem prostym pod względem podstawy (czyli prostopadłe do podstawy) graniastosłupa, np.:

b) graniastosłupy pochyłe: w tym rodzaju graniastosłupów ściany boczne (będące prostokątami oraz równoległobokami) są ułożone pod pewnym kątem (nie będącym kątem prostym) pod względem podstawy (czyli nie są prostopadłe do podstawy) graniastosłupa, np.:
To nie jest jedyny podział graniastosłupów, graniastosłupy dzielimy również ze względu na występujący w podstawie wielokąt:
a) graniastosłupy- zwyczajne graniastosłupy w, których podstawie występuje wielokąt nie będący figurą foremną, np.:
b) graniastosłupy foremne- w podstawie występuje figura foremna, np.:
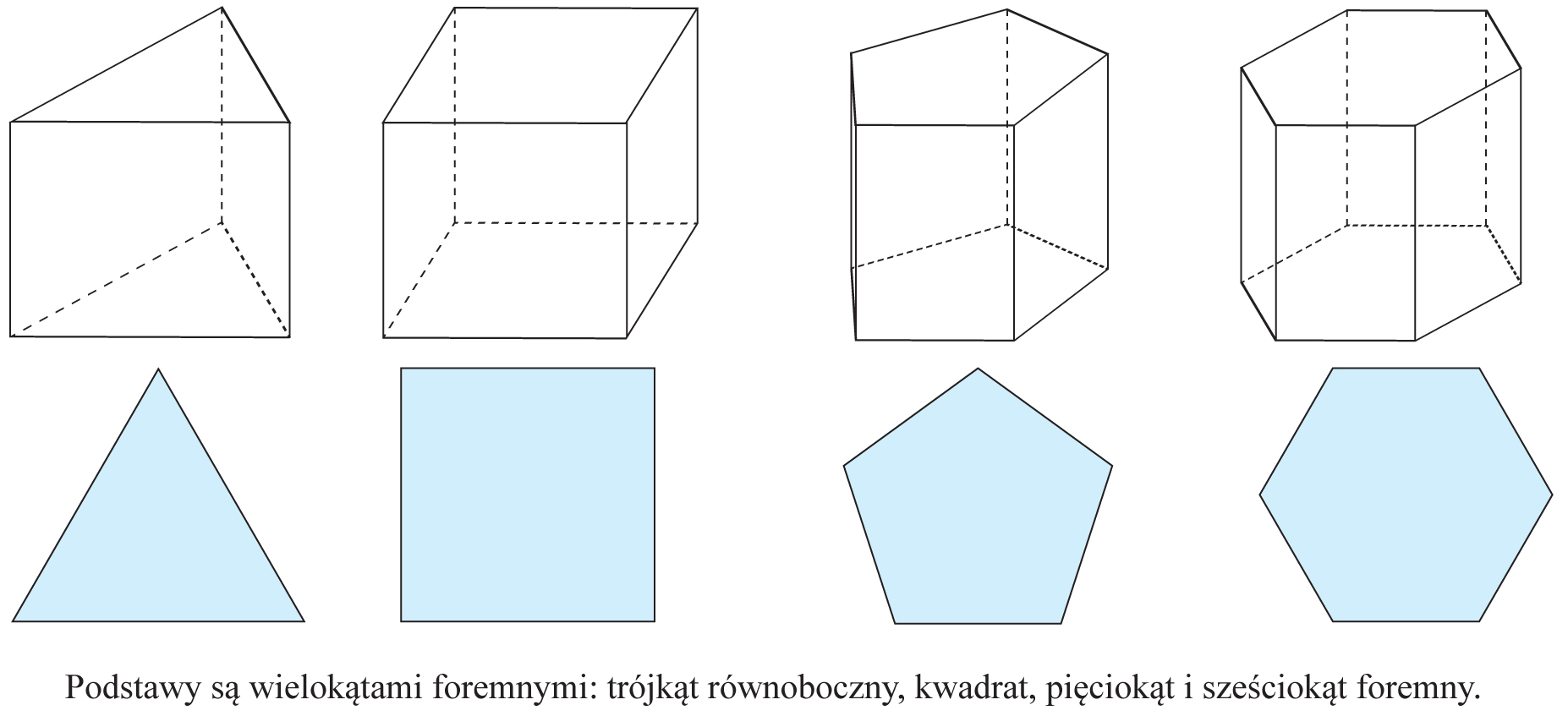
Uwaga!!!
graniastosłupy foremne są jednocześnie graniastosłupami prostymi
Możecie się teraz zastanawiać jak tworzy się nazwy graniastosłup. Otóż nazwy graniastosłupów tworzymy poprzez:
graniastosłup (1) (2-jaki?)
na początku nazwy zawsze musi występować nazwa graniastosłup, gdyż bez tego reszta członów nie będzie miała sensu (lub nie wiadomo co będzie oznaczać)
(1) rodzaj graniastosłupa:
-prosty
-pochyły
-prawidłowy (gdy graniastosłup jest prosty, a w podstawie jest wielokąt foremny)
(2-jaki?) figura występująca w podstawie (musi być), pamiętaj tylko o tym, by zmodyfikować trochę nazwę tego wielokąta, gdyż ten człon ukazuje nam cechę (czyli podstawę) graniastosłupa. Tutaj po prostu tak dopasuj nazwę wielokąta, by odpowiadał na zadane pytanie
(czyli: jaki?)
Według tego wzoru tworzy się podstawowe nazwy graniastosłupów takie jak, np.:
-graniastosłup foremny pięciokątny
-graniastosłup foremny trójkątny
Wiele (dokładnie 2) graniastosłupów możemy nazwać na kilka sposobów:
-Jeśli graniastosłup jest graniastosłupem foremnym czworokątnym i jego ściany boczne mają kształt kwadratów, to ten graniastosłup możemy nazwać sześcianem:

Przy zadaniach o sześcianie, jest podawana tylko długość jego jednej krawędzi (gdyż sześcian ma wszystkie krawędzie równej długości)
-Jeśli wszystkie ściany graniastosłupa są prostokątami (gdzie występują tylko 3 różne pary prostokątów przystających) to wtedy ten graniastosłup nazywamy prostopadłościanem :
W prostopadłościanie (i tylko u niego) jest możliwość innego przedstawienia jego wymiarów, czyli zamiast omawiać jego długości w treści zadania (lub przedstawieniu ich na obrazku prostopadłościanu), możemy napisać to w formie:
a X b X c
co oznacza:
Prostopadłościan ma wymiary: ,a’ na ,b’ na ,c’
w praktyce może to wyglądać, np. tak:
5m X 10m X 7m
co oznacza:
Prostopadłościan ma wymiary: 5m na 10m na 7m
W takim zapisie kolejność długości oznacza kolejno:
krawędź podstawy X krawędź podstawy (inna niż poprzednia) X krawędź boczna
Budowa graniastosłupa:
graniastosłup składa się z:
-podstawy (górna i dolna)
-ścian bocznych
-krawędzi bocznych
-krawędzi podstawy
-wierzchołków
W praktyce wygląda to tak:
Tutaj mogę już przytoczyć pierwsze wzoru graniastosłupa, dokładnie wzory na obliczenie:
-wszystkich wierzchołków:
W= 2n
gdzie:
W- wszystkie wierzchołki
n- liczba kątów występujących w podstawie, można to nazwać też ilością boków z których składa się wielokąt w podstawie, gdyż:
ilość kątów = liczba boków w wielokącie w podstawie)
-wszystkich krawędzi:
K= 3n
gdzie:
K- wszystkie krawędzie
n- patrz wyjaśnienie przy wszystkich wierzchołkach
-wszystkich ścian:
S= n+2
gdzie:
S- wszystkie ściany
n- patrz wyjaśnienie przy wszystkich wierzchołkach
To co widzicie to niejedyne co zawiera graniastosłup. Jak wiesz, figury mają przekątne (czyli odcinki wewnątrz wielokąta łączące 2 wierzchołki, lecz nie będące jego bokami) i właśnie graniastosłupy również je posiadają. W graniastosłupie wyróżniamy przekątne:
a) podstawy- przekątne w podstawie graniastosłupa
długość przekątnych w podstawie możemy wyliczyć albo z własności:
-dla kwadratu:
gdzie:
d- przekątna kwadratu
a- bok kwadratu
-dla sześcianu foremnego:
najdłuższa przekątna jest dwa razy większa od boku sześciokąta, a krótszą wylicza się ze wzoru:
gdzie:
d- krótsza przekątna sześcianu
a- bok sześcianu
albo z twierdzenia pitagorasa
b) ściany bocznej- przekątne oparte tylko na ścianie graniastosłupa. Żeby wyliczyć ich długość, trzeba skorzystać z twierdzenia pitagorasa lub wzoru na przekątną kwadratu (w przypadku, gdy ściana boczna jest kwadratem, patrz wyżej)
c) graniastosłupa- przekątna łącząca 2 wierzchołki podstaw górnych i dolnych. Żeby wyliczyć ich długość, musimy skorzystać z twierdzenia pitagorasa (tylko wcześniej musimy znać przekątną podstawy i wysokość, który przebiegają w tą samą stronę co przekątna i łączą te dwa wierzchołki tworząc trójkąt prostokątny)
Dla graniastosłupa istnieją jeszcze 2 wzory. Są to wzory na pole całkowite graniastosłupa i jego objętość:
-pole całkowite- służy nam obliczeniu łącznej powierzchni wszystkich ścian (łącznie z podstawami) graniastosłupa. Obliczamy ze wzoru:
gdzie:
Pc– pole powierzchni całkowitej
Pp– pole podstawy (liczmy dwukrotnie, gdyż w graniastosłupie zawsze występują dwie podstawy)
Pb– łączne pole wszystkich ścian bocznych (ze względu na to, że różne graniastosłupy posiadają inną ilość ścian bocznych)
Licząc pole całkowite pamiętaj o tym by wartości były wyrażone w tej samej jednostce (pamiętając o zamianie jednostek powierzchni)
-objętość- pojemność graniastosłupa oznaczająca ile możemy pomieścić, np.: litrów wody w graniastosłupie. Obliczamy ze wzoru:
gdzie:
V- objętość
Pp– pole podstawy
H- wysokość graniastosłupa
Tak jak przy polu całkowitym, pamiętaj o tym, by wartości były wyrażone w tej samej jednostce (pamiętając o zamianie jednostek objętości)
Możesz się zastanawiać, czemu tutaj występuje ,H’ (duże), a nie ,h’ (małe). Otóż ,h’ (małe) oznacza wysokość (tutaj oznacza odległość między najwyższym punktem figury, a podstawą przebiegającą w linii prostej prostopadłej względem podstawy) na płaszczyźnie, gdy ,H’ (duże) oznacza wysokość (tym razem jest to już dosłowne znaczenie: odległość między podstawą górną, a dolną w linii prostej, prostopadłej względem podstawy dolnej- jest tak w przypadku graniastosłupa pochyłego, w przypadku prostego jest to długość krawędzi bocznej) w przestrzeni (czasami oznaczane też jako ,y’)
Pamiętasz jeszcze o sześcianie i prostopadłościanie? Otóż te graniastosłupy posiadają uproszczone wzory na pole całkowite i objętość.
-w przypadku sześcianu:
gdzie:
a- długość krawędzi (dowolnej)
Wzór jest w takiej postaci ze względu na to że sześcian składa się z sześciu identycznych kwadratów
gdzie:
a- długość krawędzi (dowolnej)
-w przypadku prostopadłościanu:
gdzie:
a- długość krawędzi podstawy
b- długość krawędzi podstawy (nie będącej krawędzią ,a’)
c- długość krawędzi bocznej
gdzie:
a- długość krawędzi podstawy
b- długość krawędzi podstawy (nie będącej krawędzią ,a’)
c- długość krawędzi bocznej
Pamiętaj, by wartości (w obu wzorach dla prostopadłościanu) te były wyrażone w tej samej jednostce oraz zwróć uwagę na to że nawet jak obrócimy bryły i ustawimy na dowolnej ściance, to pole całkowite i objętość się nie zmienią, dlatego opisane wyżej krawędzie prostopadłościanu mogą oznaczać różne odcinki (np.: krawędź ,a’ może oznaczać krawędź boczną, gdy krawędź ,c’ będzie oznaczać krawędź podstawy), lecz przy innych graniastosłupach nie zaczynaj liczyć pola całkowitego lub objętości od ścianki na której leży graniastosłup, lepiej zacznij od wyliczenia jako pola podstawy, ścianki, która występuję dwa razy (od innego wielokąta, który nie jest prostokątem lub kwadratem)
Za chwilę przystąpię do robienia zadań, lecz za nim do tego przejdę chciałbym o czymś wspomnieć. Tym czymś jest coś takiego jak ,,siatka graniastosłupa”, to graniastosłup na płaszczyźnie, ale nie w całości, gdyż siatka przedstawia nam jego poszczególne ściany (wraz z podstawami) w takim ułożeniu, że ukazuje nam w jaki sposób są rozmieszczone poszczególne ściany graniastosłupy, np.:

Dodatkowo dzięki siatce, mamy możliwość złożenia graniastosłupa (pamiętaj tylko, by dodać jeszcze tzw.: języczki w celu, by graniastosłup się ,trzymał’ i nie rozpadł)
Teraz po tej teorii czas na zadania:
Zad. 1
Jacek chce złożyć drewniane koryto (przedstawione na rysunku obok) o wymiarach 50dm X 1m X 70dm, które nie ma górnej ściany. Oblicz ile Jacek potrzebuje m2’ drewna z którego ułoży te koryto (policz tylko powierzchnię zewnętrzną) oraz ile pomieści ono maksymalnie litrów wody?
Na początku wypiszmy dane i szukane:
Dane:
a- 50dm= 0,5m (Pamiętamy o jednakowych jednostkach, a musimy wynik podać w ,m2’)
b- 1m
c- 70dm= 0,7m
Dane jest również, że koryto nie ma górnej ścianki, więc pomijamy ją w obliczeniach oraz, że liczymy tylko powierzchnię zewnętrzną
Szukane:
Pc– ?
V-?
Rozwiązanie:
Po zapisie wymiarów tego koryta, wiemy, że ma ono kształt prostopadłościanu
Pc= 2(bc+ac) + ab (ze względu na to że jedną ściankę pomijamy, a ta ścianka pomijana jest podstawą górną)
Pc=
Wzór na objętość jest taki sam jak podawałem (różnica jest taka, że w tym przypadku łatwiej wlać wodę :)) oraz musimy pamiętać, o tym, że w zadaniu pytają nas o litry (wody), więc wynik musimy podać w litrach
(pole podstawy obliczyliśmy w poprzednim działaniu)
(Pamiętaj: 1dm3= 1L [1litr])
Ze względu na to, że jest to zadanie z treścią (oraz zadają nam pytanie) musimy napisać jeszcze odpowiedź:
Odp.: Jacek na koryto potrzebuje łącznie 2,75m2 drewna oraz w korycie pomieści maksymalnie 350L wody
Zad. 2 Przepraszam za jakość obrazka, wymiary podam w danych
Oblicz pole powierzchni całkowitej, objętość oraz nazwij graniastosłup, którego siatka jest przedstawiona obok.
Ważne!!!
Tradycyjnie rozpoczęlibyśmy od wypisywania danych, lecz obok mamy przedstawioną siatkę. Polecam wam wyobrazić sobie złożony już graniastosłup na podstawie tej siatki. W przypadku, gdy trudniej jest wam go sobie wyobrazić, naszkicujcie sobie jak, mógłby wyglądać złożony z tej siatki graniastosłup (pamiętając o występujących w siatce wielokątach)
Dane:
a- 3 (na obrazku nie ma podanych jednostek więc liczb nie są zapisywane z jednostkami, mimo, że jest narysowana na kartce w kratkę)
b- 3
c = H = 4
Szukane:
Pc= ?
V= ?
Nazwa (to też składa się na odpowiedź)
Obliczamy pole powierzchni całkowitej, lecz jak pamiętamy, najpierw obliczamy pole podstawy i łączne pole ścian bocznych, a ze względu na to, że widać, że to nie prostopadłościan, korzystamy z tradycyjnego wzoru:
(j2 oznacza jednostki kwadratowe, wykorzystujemy, gdy nie ma danych konkretnych jednostek oraz ma na celu doprecyzowaniu czego ta liczba może dotyczyć)
(mamy 4 identyczne ściany boczne, więc liczymy pole jednej ściany i wynik mnożymy przez 4)
Teraz nazwijmy ten graniastosłup:
Na siatce widzimy, że w podstawie występują kwadrat, więc człon ostatni będzie się zwał: ,,czworokątny” , a ze względu na to że kwadrat należy do figur foremnych oraz w siatce są same prostokąty, które oznaczają, że graniastosłup jest także prosty, więc możemy go również nazwać prawidłowym, więc graniastosłup ten nazwiemy:
,,graniastosłup prawidłowy czworokątny”
Gdy nie musimy dawać odpowiedzi do zadania, polecam na swoich rozwiązać zanotować wszystko o co nas pytają:
nazwa:
,,graniastosłup prawidłowy czworokątny”
Koniec

