Ćwiartki układu współrzędnych

Ogólnie
W matematyce często posługujemy się układem współrzędnych. Prostokątny układ współrzędnych, zwany również układem współrzędnych kartezjańskich tworzą dwie, prostopadłe osie liczbowe , które przecinają się w jednym punkcie zwanym początkiem układu współrzędnych. Początek jest to punkt zwykle oznaczany cyfrą 0 lub literą O. Używany jest w przestrzeni euklidesowej jako punkt odniesienia dla geometrii otaczającej go przestrzeni. Początek dzieli każdą z tych osi na dwie połowy; półoś dodatnią i półoś ujemną. Dzięki temu układowi możemy zaznaczyć i odszukać lokalizację punktów. Punkty mogą być wskazane względem początku układu współrzędnych poprzez podanie ich współrzędnych liczbowych, to znaczy pozycji ich wzdłuż każdej z osi, zarówno w kierunku dodatnim, jak i w kierunku ujemnym. Współrzędne początku są zawsze zerami, np. ( 0, 0) w dwóch wymiarach. Oś poziomą nazywamy zazwyczaj osią X, albo osią OX, rzadziej osią odciętych. Oś pionową nazywamy osią Y, lub osią OY, rzadziej osią rzędnych. Nazwa układu współrzędnych pochodzi od francuskiego matematyka i filozofa Kartezjusza ( Rene Descartes), który wprowadził tę myśl w 1637 roku. Już wcześniej, w 1636 roku Pierre de Fermat używał metody prostokątnego układu współrzędnych, ale nie opublikował tego, dlatego pozostało to nieznane. W momencie, kiedy Kartezjusz opracował układ współrzędnych powstał spór o pierwszeństwo z Fermatem. Ostatecznie sytuacja ta zakończyła się uznaniem zasług obu naukowców.

Ćwiartki układu współrzędnych
Osie dwuwymiarowego układu kartezjańskiego dzielą płaszczyznę na cztery nieograniczone i przystające zbiory zwane ćwiartkami.

Ćwiartki często numeruje się od pierwszej do czwartej i do oznaczenia używa się symboli rzymskich. Przy zwyczajnym rysowaniu numerowanie zaczyna się od prawej górnej ćwiartki, a pozostałe ćwiartki wyznacza się w kierunku przeciwnym do ruchu wskazówek zegara. Każdy punkt, który ma położenie w układzie współrzędnych określają dwie współrzędne ( x, y,). Można również znaleźć ich lokalizację poprzez przydział do odpowiedniej ćwiartki. Punktów leżących na osiach układu współrzędnych nie zaliczamy do żadnej ćwiartki. W I ćwiartce leżą punkty, których obydwie współrzędne są dodatnie ( x > 0, y > 0). Jeżeli pierwsza współrzędna jest ujemna, a druga dodatnia ( x < 0, y > 0), to takie punkty należą do II ćwiartki. Punkty nalężące do III ćwiartki, mają obie współrzędne ujemne ( x < 0, y < 0). W IV ćwiartce leżą punkty, których pierwsza współrzędna jest dodatnia, a druga jest ujemna ( x > 0, y < 0 ). Położenie punktów
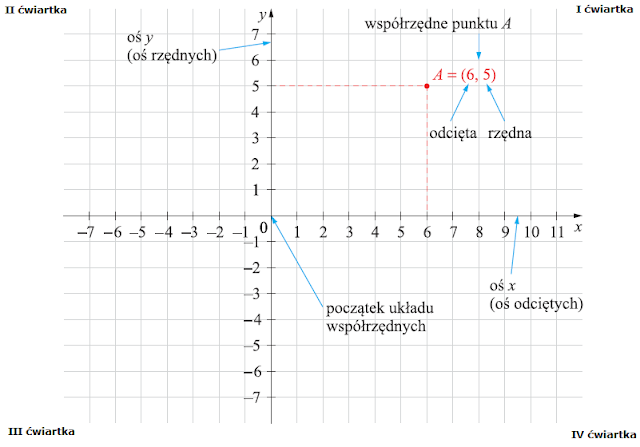
Jak już wcześniej wspomniano, położenie punktu w układzie współrzędnych określa uporządkowana para liczb ( x, y), którą nazywamy współrzędnymi punktu. Na odwrót znowu, każdej parze liczb (x, y) odpowiada w układzie współrzędnych dokładnie jeden punkt. (Pierwsza współrzędna określa położenie punktu względem osi X, a druga współrzędna- względem osi Y. Aby wyznaczyć pierwszą współrzędną ( x) punktu A, można wyznaczyć prostą prostopadłą do osi X przechodzącą przez punkt A. Liczba odpowiadająca punktowi, w którym ta prosta przecina oś X, jest pierwszą współrzędną punktu A, zwaną również odciętą punktu A. Aby wyznaczyć drugą współrzędną punktu A – współrzędną (y), można wyznaczyć prostą prostopadłą do osi Y przechodzącą przez punkt A. Liczba odpowiadająca punktowi, w którym ta prosta przecina oś Y, jest drugą współrzędną punktu A – rzędną punktu A.

A = ( x, y ) – zapisane w nawiasie współrzędne służą nam do umiejscowienia punktu w układzie współrzędnych.

Przykład

Współrzędne punktu A : pierwsza współrzędna to 1, a druga to 6. Zapisujemy A = ( 1, 6 ), punkt ten leży w I ćwiartce
Współrzędne punktu B : pierwsza współrzędna to -6, a druga to 5. Zapisujemy B = ( -6, 5 ), punkt ten leży w II ćwiartce
Współrzędne punktu C : pierwsza współrzędna to 0, a druga to 3. Zapisujemy C = ( 0,3 ), punkt ten leży na osi Y
Współrzędne punktu D : pierwsza współrzędna to 6, a druga to 2. Zapisujemy D = ( 6,2 ), punkt ten leży w I ćwiartce
Współrzędne punktu E : pierwsza współrzędna to -2, a druga to 0. Zapisujemy E = ( -2,0 ), punkt ten leży na osi X
Współrzędne punktu F : pierwsza współrzędna to 4, a druga to 0. Zapisujemy F = ( 4,0 ), punkt ten leży na osi X
Współrzędne punktu G : pierwsza współrzędna to -4, a druga to -1. Zapisujemy G = ( -4, -1 ), punkt ten leży w III ćwiartce
Współrzędne punktu H : pierwsza współrzędna to 0, a druga to -4. Zapisujemy H = ( 0, -4 ), punkt ten leży na osi Y
Współrzędne punktu I : pierwsza współrzędna to 3, a druga to -5. Zapisujemy I = ( 3, -5 ), punkt ten leży w IV ćwiartce

Zarówno przy odczytywaniu współrzędnych punktów, jak i zaznaczaniu ich, należy pamiętać, że pierwszą współrzędną należy odczytać
z osi poziomej X, a drugą współrzędną z osi pionowej Y. Najczęściej pojawiającym się błędem jest pomylenie kolejności współrzędnych. Sytuacja ta sprawia, że położenie punktu jest w zupełnie innym miejscu.

Wzory w 2- wymiarowym układzie współrzędnych
Dzięki matematykom przede wszystkim powstały również wzory pozwalające obliczyć odległości, długości, pola itp.
a) współrzędne środka odcinka AB oznaczonego literą S, gdzie A = ( a, b ), B = (c, d )
S = [( (a + c) /2 ), ( ( b + d) /2)]
2

b) odległość punktu A od środka układu współrzędnych dla A = ( a, b )

c) długość odcinka AB dla A= ( a, b ), B = ( c, d )
lub

Zastosowanie układów współrzędnych
Układy współrzędnych stosuje się również w wielu innych dziedzinach wiedzy, np. w geodezji, fizyce, geografii ( długość i szerokość geograficzna). To, o czym wspomniano to niewielka część zastosowania układu tego. W matematyce na wyższym poziomie jest dużo zadań, które bazują na układzie współrzędnych. Wszelkie mapy, gry (np. statki, szachy), nawigacje GPS wykorzystują umiejętność poprawnego lokalizowania obiektów. W życiu codziennym też spotykamy się z układem współrzędnych, chociażby poprzez wyszukanie miejsca w kinie, czy znalezienia interesującego nas towaru na półkach w dużych sklepach (np. Ikea) .