Opracowanie:
Dwusieczna kąta
Dwusieczna kąta
Kąt tworzą dwie półproste o wspólnym początku. Półproste te nazywamy ramionami kąta, a wspólny punkt, czyli początek to wierzchołek kąta. Mówiąc o kącie, można zdefiniować go jako część wspólną z brzegiem , który wyznaczany jest przez dwie proste, nierównoległe.
Dwusieczna kąta zdefiniowanego powyżej, to półprosta „p” o początku w wierzchołku takiego kąta , która dzieli ten kąt na dwa dokładnie takie same kąty, czyli na dwa kąty o jednakowych miarach. Dwusieczna kąta – czyli dosłownie – dzieląca kąt na połowy.
Dwusieczną kąta można wyznaczyć konstrukcyjnie.
Zadanie 1
Wyznacz dwusieczną kąta AOB , gdzie O jest wierzchołkiem tego kąta, a A i B są punktami leżącymi na ramionach tego kąta.
Rozwiązanie
1 . W pierwszej kolejności należy zakreślić z wierzchołka kąta „O” łuk, który będzie przecinać ramiona naszego kąta. Punkty przecięcia naszego zakreślonego łuku z ramionami naszego kąta oznaczymy punktami „A” i „B”.
2 . Mając tą samą rozwartość cyrkla, którą wyznaczyliśmy łuk (tak jak w punkcie numer 1) kreślimy dwa kolejne łuku. Jeden – wbijamy cyrkiel do punktu „A”, drugi – wbijamy cyrkiel do punktu „B”.
3 . Następnie prowadzimy półprostą z wierzchołka „O” do punktu przecięcia się łuków.
4 . Wyznaczona nowa półprosta (poniżej na rysunku zaznaczona linią czerwoną) jest naszą dwusieczną kąta, która dokładnie dzieli nasz kąt AOB na dwa równe kąty, to znaczy dwa kąty o tych samych miarach.
Dwusieczna kąta posiada następujące własności:
1 . Dwusieczna kąta jest jedyną osią symetrii danego kąta.
2 . Dwusieczna kąta płaskiego, to półprosta przechodząca przez wierzchołek kąta i dzieląca go na dwa kąty przystające.
3 . Dwusieczna kąta dwuściennego – to płaszczyzna przechodząca przez krawędź i dzieląca go na dwa kąty przystające.
4 . Każdy punkt leżący na dwusiecznej kąta , ma równe odległości od obu ramion kąta.
5 . Dwusieczna kąta leży na osi symetrii danego kąta.
6 . Dwusieczna kąta leży w obszarze danego kąta.
Spróbujmy rozwinąć troszkę punkt nr 4. Spójrz na poniższy rysunek.
Jak widzisz, został na dwusiecznej kąta zaznaczony punkt P. Co ważne, do obu ramion kąta jest ta sama odległość od tego punktu. Własność ta jest bardzo ważna podczas wykonywania wielu zadań z zakresu dwusiecznej kąta.
Warto zwrócić uwagę na dwusieczne kątów wklęsłych i wypukłych.
Poniżej ilustracje pokazujące dwusieczne powyższych kątów:
Dwusieczna kąta wklęsłego wygląda tak jak na grafice poniżej
Dwusieczna kąta wypukłego wygląda tak jak na grafice poniżej
Spróbuj teraz rozwiązać krótkie zadanie
Zadanie 2
Które z poniższych zdań mówi prawdę o dwusiecznej kąta.
1 . Dwusieczna kąta to prosta dzieląca kąt na dwa dowolne kąty.
2 . Dwusieczna kąta to półprosta prostopadła do jednego z ramion kąta.
3 . Dwusieczna kąta to półprosta dzieląca kąt na dwa równe kąty.
4 . Dwusieczna kąta to prosta prostopadła do jednego z ramion kąta i przechodząca przez jego wierzchołek.
Rozwiązanie:
Przeanalizujmy każde z powyższych zdań.
Jak wiemy, dwusieczna ma swój początek, a więc nie może być prostą – pierwsze zdanie odpada.
Dwusieczna nie jest prostopadła do ramion kąta – drugie zdanie odpada.
Dwusieczna kąta będąca półprostą, dzieli kąt na dwa równe kąty – te zdanie jest prawdziwe.
Odp. Prawdziwe zdanie to zdanie nr 3.
Zadanie 3
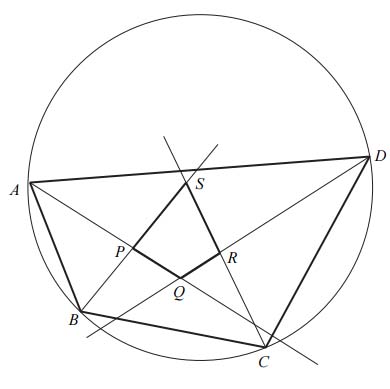
Został narysowany okrąg. W okręgu został narysowany czworokąt ABCD w taki sposób, że każdy jego wierzchołek jest na okręgu. Następnie narysowano dwusieczną każdego kąta w czworokącie. Te dwusieczne przecinają się w punktach P, Q, R, S. Udowodnij, że w czworokąt PQRS możesz wpisać okrąg, na którym będą wierzchołki czworokąta PQRS.
Rozwiązanie takiego zadania przede wszystkim rozpoczynamy od zaznaczenia kątów i ich oznaczenia. Następnie powinniśmy przypomnieć sobie informację mówiącą nam, że gdy mamy do czynienia z czworokątem wpisanym w okrąg, to suma przeciwległych kątów jest równa 180°. Na podstawie tej zależności możemy napisać następujące równania.
Tym samym możemy napisać, że suma poniższych kątów wynosi:
Widzimy, że kąty alfa i beta się upraszczają, tworząc tym samym jako wynik 180 stopni.
Z tego możemy zobaczyć, że skoro dwa kąty w czworokącie mają 180°, to pozostałe też tyle łącznie muszą mieć. Oznacza to, że tym czworokącie PQRS możemy opisać okrąg, a więc to jest to, co mieliśmy udowodnić.
C. N. U.
Na sam koniec przypomnijmy jeszcze sobie twierdzenie o dwusiecznej kąta oraz pokażmy sobie ich użycie w praktyce.
Twierdzenie o dwusiecznej kąta mówi nam, że stosunek długości boku y i do długości boku x jest taki sam jak stosunek długości boku q do długości boku z. Oczywiście, czerwona prosta to dwusieczna kąta.
Twierdzenie o dwusiecznej kąta:
Zastosowanie twierdzenia o dwusiecznej kąta w praktyce.
Zadanie 1
Oblicz długość x
Aby rozwiązać takie zadanie zaczynamy od ułożenia tego stosunku. Następnie przemnożymy na krzyż, otrzymując wynik.
Odpowiedź: x=4
Zadanie 2
Oblicz długość x
Rozwiązanie takiego zadania tym razem rozpoczynamy od wyznaczenia długości boku, który nie został oznaczony żadną literką, a więc będzie to 10 – x.
Następnie kolejny raz tworzymy stosunek.
Przemnażamy na krzyż.
Wiadome na jedną stronę i niewiadome na drugą stronę.
Dzielimy przez 12 obie strony.
Odpowiedź: Odcinek x ma długość .
Pamiętaj, że podczas rozwiązywania zadań bardzo łatwo jest pomylić boki, czy też popełnić błąd rachunkowy. Bądź czujny podczas rozwiązywania zadań. Ponadto, przy rysowaniu rysunków powinieneś/powinnaś użyć precyzji, gdyż często to właśnie dzięki rysunkom udaje nam się rozwiązywać zadania.