Wysokość trójkąta równobocznego

Dziś zajmiemy się szczególnym przypadkiem trójkąta. Jest to trójkąt równoboczny.

Co więc ma szczególnego taki trójkąt?
Ma wszystkie boki tej samej długości.
Suma kątów w trójkącie wynosi 180. Z tego wynika, że każdy z kątów w trójkącie równobocznym wynosi po 60°.
Możemy bezpośrednio ze wzoru od razu obliczyć wysokość tego trójkąta znając tylko długość jednego boku.
Możemy bezpośrednio ze wzoru od razu obliczyć pole tego trójkąta znając tylko długość jednego boku.
W tym opracowaniu jednak zwrócimy szczególną uwagę na ten pierwszy wzór. Pomimo tego, znajomość wzoru na pole trójkąta ( ) oraz wzoru na pole trójkąta równobocznego (pokazany jest powyżej) jest niezmiernie ważna. Często taką wysokość trójkąta możemy obliczyć przyrównując pole z pierwszego wzoru do pola z drugiego wzoru, tym samym możemy wyprowadzić nowy jednorazowy wzór.

Wróćmy jeszcze na chwilę do wzoru na wysokość trójkąta równobocznego. Ten wzór to: . Zastanówmy się skąd wziął się ten wzór.

Spójrz na ten trójkąt. Zapiszmy na podstawie niego twierdzenie Pitagorasa. Dążymy do wyprowadzenia wzoru na h.

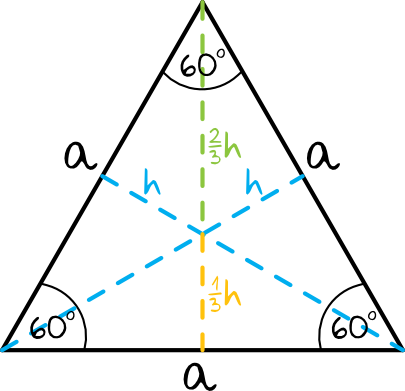
Ponadto warto wspomnieć, że wszystkie trzy wysokości tego trójkąta przecinają się w jednym punkcie. Ten punkt dzieli każdą wysokość na dwie części: oraz . Dwusieczne, a więc proste, które dzielą każdy z kątów trójkąta na dwa takie same o tej samej mierze oraz środkowe, a więc proste poprowadzone z środka boku do przeciwległego boku, przecinają się również w jednym punkcie.

Skoro wiemy już jak wyglądają podstawowe wzory, przejdźmy do zadań.

zadanie 1
Oblicz wysokość trójkąta równobocznego o boku 4cm.

I sposób rozwiązania
Narysowanie pomocniczego rysunku to pierwszy krok do rozwiązania tego zadania.

Jak widzisz, wysokość, która została opuszczona na podstawę trójkąta podzieliła go na dwa trójkąty prostokątne o przeciwprostokątnej długości 4cm oraz o przyprostokątnych h oraz 2cm. Stosując twierdzenie Pitagorasa bez problemu możemy obliczyć tę wysokość. Pamiętajmy o założeniach!!!

Założenia:
h > 0

Dane:
a = 2cm
c = 4 cm

Zapisujemy twierdzenie Pitagorasa

Podstawiamy dane do równania

Podnosimy do kwadratu wiadome nam wyrazy

Przerzucamy wiadome na prawą stronę

Rozwiązujemy prawą stronę

Zapisujemy już końcowy wynik pamiętając o tym, że każde równanie kwadratowe ma dwa rozwiązania. Dlatego właśnie były nam potrzebne założenia, które mówią nam, że wynik musi być dodatni.

Odpowiedź: Wysokość tego trójkąta wynosi .

II sposób rozwiązania

Również zaczynamy rozwiązanie tego zadania od narysowania rysunku pomocniczego.

wypiszmy sobie dane:
a = 4cm
Teraz zastosujmy po prostu nasz wzór na wysokość trójkąta równobocznego:

Zapisujemy nasz wzór oraz podstawiamy dane

Skracamy ułamek

Zapisujemy gotowy wynik

Jak widzisz, pokazałam ci dwa sposoby rozwiązania zadania. Decyzja należy do ciebie, który sposób wybierzesz. Metoda nr 2 jest zdecydowanie bardziej uniwersalna. Wzór ten przyda Ci się nie tylko przy egzaminie ósmoklasisty, lecz będzie Ci także potrzebny na maturze i na studiach.

zadanie 2
Został opisany okrąg na trójkącie, które boki są tej samej długości. Promień tego okręgu wynosi 8. Oblicz ile wynosi wysokość trójkąta.

Rozwiązanie:

Rozwiązanie takie zadania powinniśmy rozpocząć od narysowania okręgu o promieniu 8. Następnie przystępujemy do narysowania trójkąta równobocznego na tym okręgu. Następnie rysujemy każdą z trzech wysokości trójkąta. Pamiętajmy, że wysokość jest poprowadzona pod kątem prostym z boku trójkąta do przeciwległego wierzchołka. Jak zaznaczymy te wszystkie wysokości to zauważymy, że przecinają się one w jednym punkcie. Następnie przypominamy sobie zależność, że punkt przecięcia tych wysokości jest punktem, który dzieli wysokość na dwie części. Jedna część jest dwa razy dłuższa od pierwszej. W takim razie sprawdzamy, jakie mamy dane na rysunku. Jak widzisz, dwa razy dłuższy odcinek podstały po przecięciu się wysokości to nic innego jak promień naszego okręgu. W takim razie możemy zapisać, że . Powstaje nam wtedy bardzo proste równanie liniowe. Rozwiązujemy te równanie otrzymując końcowy wynik.

Obustronnie dzielimy równanie przez , a więc mnożymy przez odwrotność, czyli mnożymy przez

Odpowiedź: Wysokość tego trójkąta to 12.