Asymptoty

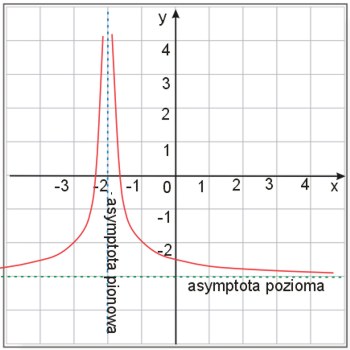
Wejdźmy w świat funkcji. Najłatwiej rzecz ujmując, asymptotą nazywamy prostą, do której zbliża się wykres. Co to więc oznacza?

Spójrz na powyższą grafikę. Im większe są wartości funkcji, tym wykres jest bliżej asymptoty pionowej. Patrząc jednak na oś X, im bliżej jesteśmy plus i minus nieskończoności, tym nasz wykres znajduje się bliżej asymptoty poziomej.

Podsumowując, wyróżniamy asymptoty:

1 . Pionowe

2 . Poziome

3 . Ukośne

Generalnie rzecz ujmując, bardzo często gdy mamy asymptotę pionową, to występuje też i pozioma asymptota. Co ważne, wykres może także przecinać się z asymptotą. Chyba że mówimy o specjalnych funkcjach (np. w funkcjach homograficznych), w których wykres NIGDY NIE DOCHODZI do asymptot. Ponadto, w niektórych przypadkach wykres może się pokrywać z asymptotą.

Powyżej pokazałam jak wyróżnić asymptotę pionową, poziomą, czy też ukośną. Spróbuj teraz przeanalizować sam poniższe grafiki, tym samym sprawdzając siebie samego. Określ, jakie występują na każdym z wykresów asymptoty. Na końcu opracowania znajdziesz odpowiedzi.
1 .

2 .

3 .

4 .

5 .

6 .

Jak więc się pewnie domyślasz, równanie każdej asymptoty, czy też jej przecięcie z osią X oraz z osią Y można policzyć. To jest jeden dosyć skomplikowany temat, a takie obliczenia będziesz pewnie wykonywać dopiero na studiach. Będąc w szkole średniej, asymptoty zazwyczaj są wyznaczane przez wektor przesunięcia wykresu np. funkcji homograficznej. Jednakże, poniżej pokaże Ci, na czym polegają te asymptoty. Nie przerażaj się tymi trudnymi „znaczkami”. Z czasem je zrozumiesz.

Asymptotę pionową a funkcja f(x) wtedy i tylko wtedy, gdy:

x = a oraz gdy:

Przykłady:

Asymptotę ukośną ma funkcja f(x) wtedy i tylko wtedy, gdy:
oraz gdy:

Przykłady:

Asymptotę poziomą, a więc szczególny przypadek asymptoty ukośnej może nastąpić, gdy:
Jeżeli to zachodzi, to asymptota pozioma jest postaci: , gdy:

Przykłady:

Odpowiedzi do ćwiczenia:
Asymptota pionowa i pozioma (wykres „nie dochodzi” do asymptot).
Asymptota pozioma i dwie asymptoty pionowe (wykres „nie dochodzi” do asymptot).
Asymptota ukośna (wykres „nie dochodzi” do asymptot).
Asymptota ukośna oraz pionowa (wykres „nie dochodzi” do asymptot).
Asymptota pozioma (wykres przechodzi przez tę asymptotę).
Dwie asymptoty ukośne (pokrywają się z wykresem).