Opracowanie:
Cosinusoida
Cosinusoida
Cosinusoida jest wykresem funkcji cosinus, a więc jednej z czterech funkcji trygonometrycznych. W związku z tym, że funkcja ta jest traktowana jako funkcja zmiennej rzeczywistej, wzór jej przedstawia się następująco:
, gdzie x jest miarą kąta.
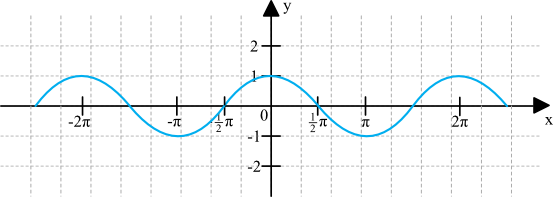
Wykres ten prezentuje się następująco:
Zauważ, że wykres ten przedstawia „falę”. W związku z tym, bez problemu możemy odczytać z wykresu częstotliwość, amplitudę (wychylenie z położenia równowagi) oraz okres tej funkcji ( od 0 do 360 stopni to jeden okres naszej funkcji, a więc 2π). W takim razie, funkcję tę będziemy nazywać funkcją okresową.
Spójrz na oś y. Na tej osi możemy odczytać wartości, jakie przyjmuje ta funkcja. Co ważne, wartości te zaczynają się na minus 1, a kończą na jedynce.
Jeśli chodzi o okres, to bardzo łatwo go wyłapać. Wystarczy znaleźć powtarzający się element.
Element oddzielony zielonymi prostymi (oraz czerwonym odcinkiem) jest jednym okresem naszej funkcji.
Spójrz na oś x naszego wykresu. Jak widzisz, mamy tam podziałkę, która jest wyrażona nie w stopniach. Jest ona wyrażona w radianach, które silnie łączą się ze stopniami. Ich zależność pokazuje poniższe równanie:
Mając tę zależność bez problemu poprzez stworzenie proporcji, zawsze możemy zmienić radiany na stopnie lub też stopnie na radiany.
CZAS NA SZKICOWANIE WYKRESU!!!!
Gdybyśmy chcieli własnoręcznie naszkicować taki wykres, konieczna byłaby znajomość wartości cosinus dla kątów ostrych, a więc od 0 stopni do 90 stopni. Po zaznaczeniu odpowiednio punktów, łączymy je tworząc część wykresu. Rysując ten wykres powinno wyjść tobie coś takiego,
Następnie otrzymaną czarną część wykresu symetrycznie rysujemy poniżej osi x. Kolejno rysujemy symetrycznie całą drugą połowę okresu tej funkcji. Takim oto sposobem, powtarzając te czynności możemy otrzymać wykres funkcji cosinus.
Koniec końców, otrzymujemy wykres podobny do tego co powyżej.
Co możemy odczytać z wykresu funkcji cosinus?
Przede wszystkim wykres ten w pewien sposób może zastąpić nam tablice trygonometryczne, gdyż mając wykres nie jesteśmy ograniczeni miarą kąta, którego będziemy brali pod uwagę. W takim razie, z tego wykresu możemy odczytywać wartości funkcji trygonometrycznej cosinus dla każdego (dowolnego) kąta.
Wzory redukcyjne, a więc wzory których jest dosyć sporo, a które pomagają nam w obliczeniach przy dużych miarach kątów, również są możliwe do wyprowadzenia poprzez skorzystanie z wykresu. Jak wiesz, wzory redukcyjne pozwalają nam przejść z kątów o dużych miarach, na obliczenia na małych miarach kątów. Przykładowo, chcąc obliczyć ile wynosi cosinus 150° wystarczy, że wyrazimy tę miarę w radianach, a następnie znajdziemy tę miarę łukową kąta na osi x. Następnie szukamy, dla jakiej innej miary kąta, wykres przyjmuje tę samą wartość. W tym przypadku cosinus 150 stopni wyniesie tyle samo co cosinus 30 stopni, tyle tylko, że zmieni nam się znak (cosinus 30° jest dodatni, a cosinus 150° jest ujemny, co wynika z wykresu).
Ponadto wykresy znacznie ułatwiają nam rozwiązywanie nierówności oraz równań trygonometrycznych.
zadanie 1
Oblicz korzystając z wykresu, ile wynosi cosinus 270°.
Rozwiązanie takiego zadania zaczynamy od przeliczenia stopni na radiany:
180° —>
270° —> x
Szukamy tego argumentu na wykresie. Następnie szukamy w tej samej linii prostej punktu. Znajdujemy , co jest równoważne z kątem 90°, dla którego wiemy, że cosinus wynosi 0. W takim razie kąt 270° dla funkcji cosinus przyjmuje wartość 0.
Na sam koniec warto jeszcze dla pewności sprawdzić to, czy aby na pewno dobrze pamiętaliśmy wartość cosinusa dla 90°.
Odpowiedź: Cos 270° wyniósł 0.