Cos 45

Cosinus kąta równego 45 stopni wynosi . Zgodnie z odczytem z tablic trygonometrycznych wynosi 0,7071. Cosinus to jedna z funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym.

Na podstawie powyższego rysunku możemy zdefiniować co oznacza cosinus kąta , który jest jednym z dwóch kątów ostrych w trójkącie prostokątnym, których suma kątów wewnętrznych wynosi 180°. Jest to stosunek przyprostokątnej leżącej przy kącie (zwanej również przyprostokątną przyległą) do przeciwprostokątnej.

Poniżej tabela przedstawiająca wartości funkcji cosinus i sinus dla często używanych w zadaniach matematycznych miar kątów:

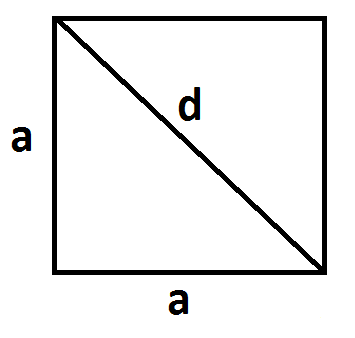
Ale skąd nam się wzięła ta dokładna wartość, oczywiście oprócz tego, że z trójkąta równoramiennego prostokątnego? A no stało się to poprzez narysowanie przekątnej w kwadracie o boku a.

Jak wiesz, z twierdzenia Pitagorasa możemy obliczyć długość przekątnej d. Ona wynosi . W związku z tym, że przekątna ta dzieli kwadrat na dwa trójkąty równoramienne o boku a (trójkąt 45°, 45°, 90°). Bez problemu możemy pokazać, że cosinus 45 stopni wynosi dokładnie tyle, ile podałam powyżej.

Dane:
przyprostokątna przy kącie – a
przeciwprostokątna –

Jeśli więc spotkasz się z zadaniem, w którym masz udowodnić słuszność tej wartości cosinusa, możesz albo udowodnić to rysując trójkąt równoramienny prostokątny, lub też możesz skorzystać z kwadratu oraz z jego przekątnej.

Ponadto, tę wartość możesz także znaleźć na wykresie funkcji cosinus.

Jak widzisz, na osi x mamy zapisane wartości w radianach, więc wystarczy zamienić radiany na stopnie lub na odwrót, i dzięki temu będziemy mogli znaleźć szukaną przez nas wartość.

Zadanie, które sprawdzi to, czy dobrze potrafisz zastosować powyższą wiedzę:
Wyznacz wartość ułamka: dla danego trójkąta prostokątnego , w którym przyprostokątna leżąca przy kącie ostrym alfa ma długość oraz przeciwprostokątna ma długość . Wiadomo, że

Jeżeli Z równania wyznaczymy zmienną :

Następnie wartość wyliczonej zmiennej podstawimy do naszego wyrażenia ułamkowego:

Odpowiedź: wartość wyznaczonego ułamka wynosi .

Zadanie:
W trójkącie równoramiennym prostokątnym ramię wynosi 2 cm. Oblicz kąt ostry między podstawą a ramieniem oraz oblicz cosinus tego kąta.

Kąty przy podstawie mają tę samą miarę. Skoro suma kątów wewnętrznych w każdym trójkącie wynosi 180°, to:

180° – 90° =

Spróbujmy najpierw te zadanie rozwiązać na „literkach”, a więc będzie to taki szablon. Oznaczmy ramiona jako a, a przeciwprostokątną jako c. Zastosujmy twierdzenie Pitagorasa:

zapisujemy twierdzenie

sumujemy prawą stronę

obustronnie pierwiastkujemy

otrzymujemy długość przeciwprostokątnej uzależnioną od długości ramienia

W takim razie,

Zauważ, że we wzorze na cosinus użyłam literki a, co wynika z naszych oznaczeń z zadania. Jak widzisz, nie musieliśmy podstawiać tutaj długości ramienia, gdyż długości boków nam się skróciły.

Oczywiście, mogliśmy podstawić długości naszych boków, a więc a = 2 oraz kąt alfa ciągle wynosi 45 stopni: