Elipsoida

Powierzchnia, w której w każdym wymiarze (x, y, z), a więc w każdym przekroju płaskim jest elipsa, to nic innego jak elipsoida. Innymi słowy, jest to po prostu bryła, w której każdy płaski przekrój stanowi elipsa.

Oczywiście, możemy spotkać się ze szczególnymi przykładami elipsoidy. Takim przypadkiem jest przede wszystkim elipsoida obrotowa. Obrót wokół osi własnej elipsy stanowi ograniczoną powierzchnie tej elipsoidy. Oznacza to więc, że przynajmniej 2 półosie są tej samej długości.

Powyżej 2 pół osie są tej samej długości, a poniżej wszystkie półosie są różnych długości.

Wyróżniamy elipsoidę spłaszczoną (obrotową) oraz elipsoidę wydłużoną (obrotową).

elipsoida obrotowa spłaszczona
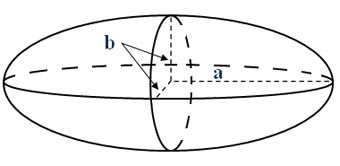
elipsoida obrotowa wydłużona

Gdy mówimy o szczególnym przypadku elipsoidy, w którym wszystkie półosie są tej samej długości, a więc , to mówimy o sferze, której promień jest długości a.

Skoro mówimy o bryle, to możemy oczywiście obliczyć jej objętość. Ja pokaże wzory dla szczególnych przypadków tych brył:

1 . Aby obliczyć objętość elipsoidy obrotowej wydłużonej, to musimy znać długość półosi a oraz b. Tutaj oczywiście dwie z trzech półosi są tej samej długości (b=c).

Wzór ten to:

2 . Aby obliczyć objętość elipsoidy obrotowej spłaszczonej, to musimy znać długość półosi a oraz b. Tutaj oczywiście dwie z trzech półosi są tej samej długości.

Wzór ten to:

W ramach ćwiczenia, spróbuj obliczyć objętość elipsoidy obrotowej spłaszczonej o półosiach 1 oraz 2. Rozwiązanie takiego zadania jest bardzo proste, gdyż wystarczy tylko podstawić dane do wzoru.