Opracowanie:
Sin 60 stopni
Sin 60 stopni
Zacznijmy od przedstawienia czym jest sinus i podania jego definicji. Żeby zrozumieć treść tej definicji musimy przypomnieć jakie nazwy mają boki w trójkącie prostokątnym.
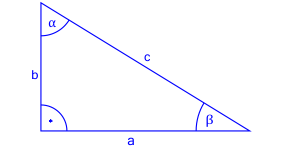
Dwa boki, które przylegają (stykają się) do kąta prostego, czyli tego o mierze 90 stopni nazywamy przyprostokątnymi, natomiast długość boku, który leży naprzeciwko tego kąta to bok o nazwie przeciwprostokątna.
Przeciwprostokątna jest najdłuższa ze wszystkich trzech boków.
Przedstawmy nazewnictwo tych boków na rysunku.
Przedstawmy teraz definicję sinusa.
Sinus to stosunek długości przyprostokątnej leżącej naprzeciwko kąta, którego chcemy obliczyć sinus do długości przeciwprostokątnej.
Wartość sinusa jest dodatnia dla kątów o mierze od 0 do 90 stopni, a także dla kątów o mierze od 90 do 190 stopni.
Podajmy zatem sinus kątów na poniższym rysunku.
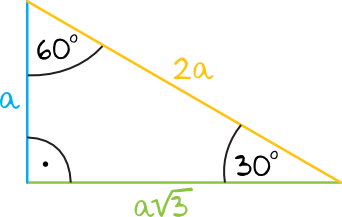
Żeby obliczyć i podać sinus kąta o mierze 60 stopni możemy skorzystać z trójkąta charakterystycznego, którego kąty mają miarę 30,60,90, a także korzystając z zależności między bokami w takim trójkącie. Przypomnijmy je:
Naprzeciwko najmniejszego kąta, czyli tego o mierze 30 stopni leży najkrótszy bok, czyli bok o długości „a”.
Naprzeciwko średniego kąta, czyli tego o mierze 60 stopni leży bok średniej długości, czyli bok o długości .
Naprzeciwko największego kąta, czyli kąta prostego o mierze 90 stopni leży najdłuższy bok, czyli bok o długości 2a.
Przedstawmy te zależności na rysunku, a następnie korzystając z definicji sinusa i tych zależności podajmy sinus 60 stopni.
Obliczmy teraz sinus kąta 60 stopni.
Skróćmy „a”.
Sinus kąta o mierze 60 stopni jest równy cosinusowi kąta o mierze 30 stopni.
Żeby to udowodnić przypomnijmy czym jest cosinus.
Cosinus to stosunek długości przyprostokątnej przylegającej do tego kąta do długości przeciwprostokątnej.
Skróćmy „a”.
Mam nadzieję, że sinus, a w szczególności sinus kąta 60 stopni nie będzie już dla Was zagadką.