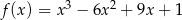Analiza matematyczna

Analiza matematyczna

Analiza matematyczna obejmuje wiele działów matematyki i jest bardzo ważna. Między innymi ważna jest tutaj umiejętność obliczania granic, czy wyznaczanie przedziałów monotoniczności.

Oprócz tego, możemy się spotkać z zadaniem optymalizacyjnym, w którym trzeba ustalić wzór funkcji z polecenia -> następnie określić dziedzinę -> wyznaczyć pochodną -> przyrównać do zera i wyznaczyć miejsca zerowe -> nasza funkcje ograniczyć do dziedziny -> stworzyć tabelkę zmienności monotoniczności funkcji -> napisanie odpowiedzi.

Przy analizie matematycznej może spotkać się również z takimi pojęciami jak :

minimum lokalne – wartość funkcji, która osiąga najmniejszą wartość w najbliższym otoczeniu
maksimum lokalne – wartość funkcji, która osiąga największą wartość w najbliższym otoczeniu
maksimum globalne – wartość funkcji, która osiąga największa wartość
minimum globalne – wartość funkcji, która osiąga najmniejszą wartość

Przykładowe zadania z objaśnieniem rozwiązania:
Wyznacz przedziały monotoniczności funkcji
Na początku trzeba obliczyć pochodną z funkcji powyżej -> teraz przyrównujemy do zera i obliczamy miejsca zerowe:
/:3

a=1 b=-4 c=3


i

teraz rysujemy wykres funkcji

A więc z wykresu możemy odczytać, że nasza funkcja:
jest rosnąca dla
jest malejąca w przedziale

Kolejne zadanie z działu analiza matematyczna:

Oblicz granicę funkcji

Aby obliczyć granicę przy x dążącym do 2, podstawimy do wzoru 2 i otrzymujemy

zatem musimy coś zmienić w naszym początkowym wzorze, w liczniku można zauważyć wzór skróconego mnożenia (a-b)(a+b)=(x+2)(x-2)
a mianownik doprowadzamy do postaci iloczynowej i zaczniemy od liczenia delty :
a= 1 b=-5 c=6



f(x)=(x-2)(x-3)

Teraz możemy cału lim zapisać jako teraz możemy skrócić nawiasy (x-2) i otrzymamy taki ułamek lim x->2 = teraz możemy za x podstawić 2 i otrzymamy

W ten sposób obliczyliśmy granicę funkcji 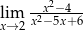, która wynosi -4.

Kolejne zadanie tym razem na poziomie podstawowym:

Aby zaznaczyć prawidłową odpowiedź musimy prześledzić nasz wykres funkcji i sprawdzić dla jakiej wartości nasza funkcja ma dokładnie trzy rozwiązania, w tym przypadku będzie to odpowiedź C – f(x)=2, gdyż ma rozwiązania w punktach na lini y=2 .

Kolejne zadanie :

Tutaj musi skupić się na początku kiedy funkcja jest stała?
Wzór funkcji liniowe wygląda tak -> f(x)=ax+b i aby ta funkcja była stała współczynnik a musi wynosić zero, więc zaczniemy od ułożenia równania które nam wyzeruje równanie przy x , zatem:
m-1=0
m=1
Naszym rozwiązaniem jest odpowiedź A.m=1

Kolejne zadanie:

Tutaj musimy zacząć od sprawdzenia monotoniczności funkcji – czyli kiedy jest malejąca, rosnąca czy też stała.
Nasza funkcja jest malejąca w przedziale:
rosnąca:
stała :
A więc naszą odpowiedzią do zadania będzie C.(1,3).