Arcus tangens

Arcus tangens tak jak arcus sinus, arcus cosinus i arcus cotangens są funkcjami cyklometrycznymi, czyli odwrotnymi do funkcji trygonometrycznych (odpowiednio tangens sinus, cosinus, cotangens), dlatego tak samo jak funkcje trygonometryczne będą one ciągłe i różniczkowalne.

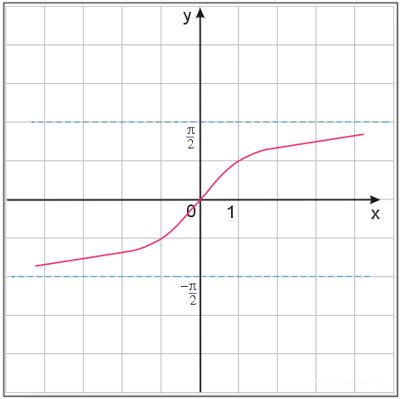
Wykres funkcji:

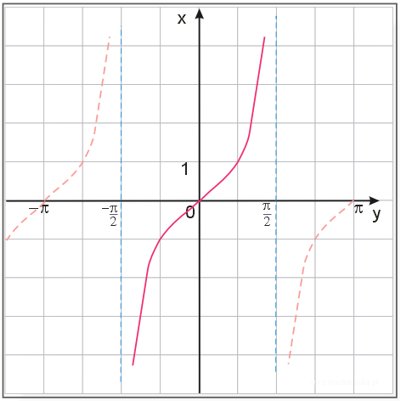
Można zadać pytanie dlaczego wykres funkcji arcus tangens jest taki 'krótki’? skoro wykres funkcji tangens przedstawia się tak:

Otóż warunkiem na istnienie funkcji cyklometrycznej danej funkcji jest jej monotoniczność. Funkcja ta musi być rosnąca lub malejąca. Jak wiemy funkcja tangens jest monotoniczna tylko przedziałami.

Zatem dzięki ograniczeniu funkcji do przedziału , na którym jest rosnąca, warunek zostanie spełniony.
, arctg(x),

po obrocie w przestrzeni
Arcus tangens jest funkcją rosnącą, rożnowartościową.

Zbiorem wartości (przeciwdziedzina) funkcji arctg(x) jest przedział otwarty (czyli przedział, do którego ograniczyliśmy dziedzinę funkcji tg(x))
Dziedziną funkcji arctg(x) jest przedział otwarty , zatem zbiór liczb rzeczywistych (czyli zbiór wartości funkcji tg(x))

arctg

arctg

arctg

Pochodna arctg(x)

(arctg(x))’

Całka arctg(x)

Przy obliczaniu wartości kąta w arctg(x) przyda się nam fakt:
arctg(x)

Przykładowo mamy do policzenia arctg( ), korzystamy z powyższego i mamy:

arctg( )

a wiemy, że , więc szukamy y t, że

Zatem wynik to

Zadanie 1.
Spróbuj obliczyć ile będzie równe arctg( )

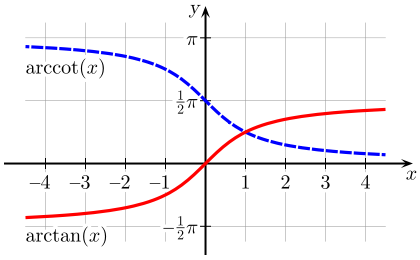
Zależności między funkcją arcus tangens i innymi funkcjami cyklometrycznymi:
> arctg = , > 0

> arctg = , > 0

> arctg + arcctg = ,

> arctg = arctg

> arctg , , dla

Zadanie 2. Oblicz arctg
Zaczynam od policzenia
Zatem arctg
Obliczamy tak jak w poprzednim zadaniu arctg
a więc