Asymptoty funkcji

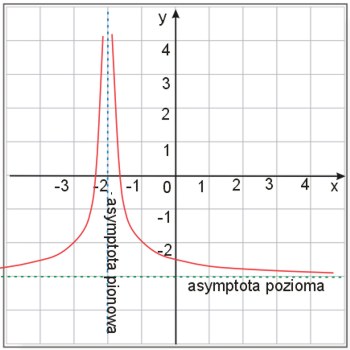
Zacznijmy od tego, że asymptoty funkcji (dokładnie asymptoty wykresu funkcji) są to proste (najczęściej przedstawiane są jako proste przerywane), które ograniczają przebieg wykresu funkcji (funkcja wtedy się nie przedłuża po stronie asymptoty, tylko ,,idzie” ku niej, a potem wzdłuż niej przebiega dalej) w układzie współrzędnych. Można to też powiedzieć, jako, że asymptota funkcji to prosta, do której ,,przytula się” wykres funkcji, która pozwala jej tylko ,,iść” po prostej wyznaczonej, co przedstawia poniższy układ współrzędnych wraz z rodzajami asymptot:

Jak widać na obrazku asymptoty są bardzo blisko wykresów (mogą się nawet z nimi przecinać lub pokrywać), ale trzeba też pamiętać, że asymptota musi przebiegać z dala od początku układu (nie może przebiegać przez ,,skrzyżowanie” wykresu, czyli przez punkt 0;0 ) choć zdarzają się wyjątki. W przypadku, gdy asymptota nie ogranicza żadnego wykresu, wtedy asymptota jest przedstawiany w postaci:
–∞ lub ∞ (znak przed nieskończonością zależy od poziomu)
Jeśli asymptota ogranicza jakąś funkcje wtedy asymptota ma postać punktu w którym asymptota ogranicza funkcję

Rodzaje funkcji:
a) Asymptota pionowa:
Tutaj funkcja f(x) posiada asymptotę pionową x=a (x- punkt współrzędnej przez który przechodzi asymptota zależny od ,,ramienia” do którego jest prostopadła asymptota) w przypadku, gdy:

lim f(x) = + ∞ oraz lim f(x) = + ∞
-> x->

Żeby znaleźć asymptoty funkcji należy obliczyć granicę funkcji w punktach, które nie należą do dziedziny funkcji (działa to tylko dla asymptot pionowych).

b) Asymptota ukośna:
Tutaj funkcja f(x) posiada asymptotę ukośną równą y= Ax + B; w przypadku gdy:
lim = A oraz lim [f(x)- Ax]= B
x->+∞ x->+∞
Dodatkowo wyróżniamy jeszcze asymptotę ukośną lewostronną [dla wykresu funkcji: y=f(x)], która występuje, gdy Df jest zbiorem, który jest nieograniczony od dołu oraz, gdy różnica wartości funkcji f(x) i funkcji liniowej ax+b w –∞ jest równa (!!!) 0; czyli:
lim [f(x)-(ax+b)] = 0
x->-∞

c) Asymptota pozioma:
Zanim przejdę do postaci asymptoty poziomej muszę dodać, że asymptota pozioma to szczególny przypadek asymptoty ukośnej, która w odróżnieniu od asymptoty ukośnej, jest prostopadła (gdy wystąpi) do asymptoty pionowej.

Tutaj jest już zależność taka, że jeżeli:

lim = 0
x->+∞
To funkcja f(x) posiada wtedy asymptotę y=B
w przypadku, gdy zachodzi równość:
lim f(x)= B
x->+ ∞

Pamiętaj tylko, żeby przy tych zadaniach zwrócić uwagę na naszą f(x), bo trzeba będzie przy niej jeszcze określić zbiór (R)

Koniec