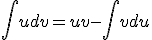Całkowanie przez części

Całkowanie przez części to jedna z metod całkowania, wykorzystywana bardzo często w matematyce w celu obliczania zamkniętych form całek.

Teraz jakiś prawdziwy wzór z całkowania przez części, który brzmi tak: Jeżeli funkcje 'u’ i 'v’ są funkcjami zmiennej 'x’ i posiadają ciągłą pochodną, to prawdziwy jest wzór:

ta metoda całkowania nosi nazwę całkowania przez części.

W zadaniach gdzie funkcje mają ciągłe pochodne, to obliczenia można zrobić na kilka sposobów:
∫f(x)⋅g′(x)dx = f(x)⋅g(x)−∫f′(x)⋅g(x)dx albo ∫f′(x)⋅g(x)dx = f(x)⋅g(x)−∫f(x)⋅g′(x)dx

A teraz zadania dla utrwalenia tego zagadnienia

Zad. 1
Oblicz całkę:
,,∫x2exdx.”
Z pomocą całkowania przez części.
Rozwiązanie:
∫x2exdx=∫x2exdx=
=∫x2(ex)′dx=
=x2ex−∫2xexdx=
=x2ex−(2xex−∫2exdx)=
=x2ex−2xex+2ex+C=
=ex(x2−2x+2)+C

I tak rozwiązaliśmy pierwsze zadanie za pomocą całkowania prze części.

Zad. 2
Oblicz całkę (od następnego zadania nie będę pisał treści zadania, bo będzie wiadome, że trzeba będzie obliczyć całkę)
∫xexdx = ∫xexdx=
=∫x(ex)′dx=
=xex−∫(x)′exdx=
=xex−∫1⋅ex=
=xex−ex+C

Przy zadaniach z całkowaniem przez części niektóre wartości możemy przyjąć jakby zachodziły pomiędzy równymi wartościami w całce:

Zad. 3
∫x cos4xdx

Przy tej całce przyjmijmy, że: { f (x)= x || f’ (x)= 1 || g’ (1) = cos4x || g (x) = sin4x
/////////////////////
Informacja:
W zadaniach (takich jak, np.: to, które teraz rozwiązujemy) możemy skorzystać ze wzoru na całkowanie przez części:
∫f (x) g’ (x) dx = f (x) g (x) – ∫f’ (x) g (x) dx
\\\\\\\\\\
Rozwiązanie:
∫x cos4xdx=
= x sin4x – ∫1 sin4xdx= x sin4x – ∫sin4xdx=

= x sin4x – (- cos4x) + C

= x sin4x + cos4x + C

A więc:
∫ x cos4xdx = x sin4x + cos4x + C
Zapamiętaj !!!!
W zadaniach (takich jak, np.: to powyżej) możemy skorzystać ze wzoru na całkowanie przez części:
∫ f (x) g’ (x) dx = f (x) g (x) – ∫ f’ (x) g (x) dx
!!!!!!!!!!!!!!!!!!!!!!!!!

Zad. 4
∫sin(lnx)dx.

∫sin(lnx)dx=∫(x)′sin(lnx)dx=
=xsin(lnx)−∫x(sin(lnx))′dx=
=xsin(lnx)−∫xcos(lnx)xdx=
=xsin(lnx)−∫cos(lnx)dx=
=xsin(lnx)−∫(x)′cos(lnx)dx=
=xsin(lnx)−(xcos(lnx)−∫x−sin(lnx)xdx)=
=xsin(lnx)−xcos(lnx)−∫sin(lnx)dx

Zad. 5
∫ In xdx

przyjmijmy, że { f (x) = In x ||| f’ (x) = |||| g’ (x) = 1 ||| g (x) = x }

Znowu skorzystamy ze wzoru (ten sam co omówiłem w poprzednim zadaniu)

∫ In xdx = ∫ 1 In xdx = (na potrzeby zadania trzeba tak zrobić [ przekonasz się później])
= In x x – ∫ xdx =
= xInx – ∫ 1dx=
=xInx – x + C

UWAGA!!!!!
Zapamiętaj ten wzór ( ∫In xdx = xInx – x + C ), gdyż jest on często wykorzystywany w zadaniach o całkowaniu przez części.
!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!

zad. 6
∫ x2 sin5xdx

Przyjmijmy, że { f(x) = x2 ||| f’ (x) = 2x ||| g'(x) = sin5x ||| g (x) = – cos5x }

∫ x2 sin5xdx = x2 ( cos5x) – ∫ 2x dx =

= – ∫ x cos5xdx

!!!!!!!!!!!!!!!!!!!
ze względy na to, że w całce znalazło się / x2 to musimy jeszcze raz musimy całkować przez części, lecz tym razem wyrażenie ∫ x cos5xdx .
A więc musimy (znowu) przyjąć, że: [{ f(x)= x /| f'(x)= 1 |/ g'(x)= cos5x /| g(x)= }]

Teraz rozwiążmy drugą część całki:
∫ x cos5xdx =

=

=

=

Teraz możemy podstawić to do wyniku z podpunktu pierwszego i kontynuować całkowanie.
∫ x2 sin5xdx = –x2cos5x – ∫ x cos5xdx

= + C1 =

=

A więc ostatecznie otrzymujemy :
∫ x2 sin5xdx =

A teraz zadanie inne niż poprzednie:

Zad. 7
∫ x In (1+x2) dx

Najpierw trzeba zrobić podstawienie:
x2+1 = t
2xdx = dt
dx =

Teraz wstawiamy to do całki:

∫ x In (1+x2) dx = ∫x In t ∫In tdt

Teraz korzystamy ze wzoru z zadania 5 (pamiętaj o nim!! )

∫ x In (1+x2) dx = ∫In tdt=

= (t In t – t + C )=

= (t In t – t ) + C =

= [(x2+ 1) In (x2+ 1 ) – (x2 + 1 )] + C2

Rozwiązanie zostawiamy w takiej formie.

Koniec