Cos 30

Cos 30 – to wartość funkcji trygonometrycznej dla kąta o mierze 30 stopni, która wynosi . Funkcja trygonometryczna dotyczy trójkąta prostokątnego, w którym boki tworzą dwie przyprostokątne oraz przeciwprostokątna. Przyprostokątne mają wspólny punkt i leżą przy kącie prostym, czyli kącie o mierze 90°, a przeciwprostokątna leży naprzeciw kąta prostego. Wartości funkcji trygonometrycznych dotyczą kątów ostrych w trójkącie prostokątnym. Na poniższym rysunku jeden z kątów oznaczymy literką . Oznacza to, że nasze rozważania dotyczące cos 30° będą dotyczyć naszego oznaczonego kąta. Dodatkowo przyprostokątne oznaczono literami a i b , a przeciwprostokątną literą c . Przybliżona wartość cosinusa 30 stopni wynosi 0.86602540378, ale częściej używana to 0.866.

Definicje funkcji trygonometrycznych względem kąta :
1 . Sin – czytaj „sinus” to stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej.

2 .cos – czytaj „kosinus” to stosunek przyprostokątnej leżącej przy kącie do przeciwprostokątnej.

3 . tg – czytaj „tangens” to stosunek przyprostokątnej leżącej naprzeciw kąta do przyprostokątnej leżącej przy kącie

4 . ctg – czytaj „kotangens” to stosunek przyprostokątnej leżącej przy kącie do przyprostokątnej leżącej naprzeciw kąta

Poniżej przedstawiono wartości funkcji trygonometrycznych dla najczęściej spotykanych kątów;

Zauważ pewne powiązanie między sinusem i cosinusem, oraz między tangensem i cotangensem.

Gdy kąt ma miarę 30 stopni, to kąt ma 60 stopni. Tym samym, jeśli wypiszemy funkcje trygonometryczne dla kąta oraz , to zauważymy, że;

Jeśli więc cosinus kąta 30 stopni , to sinus kąta 60° będzie miał tę samą wartość. Taka zależność oczywiście będzie zachodzić zawsze w kątach trójkątów prostokątnych.

Funkcje trygonometryczne służą przede wszystkich do rozwiązywania trójkątów. Dzięki tym funkcjom można obliczyć wszystkie kąty i boki trójkąta prostokątnego.

Zadanie:
Mając dany sześcian o boku oblicz cos kąta ostrego pomiędzy przekątną w sześcianie, a jego podstawą. Sprawdź, czy cosinus tego kąta jest równy co do wartości cosinusowi 30°.

Najpierw należy sporządzić rysunek poglądowy:

Zaznaczony na rysunku trójkąt o bokach jest trójkątem prostokątnym.
to przekątna podstawy sześcianu, czyli kwadratu, a z jego własności wynika, że
to przekątna sześcianu – z własności sześcianu wiemy, że
to szukany kąt
cos kąta – to stosunek przyprostokątnej leżącej przy tym kącie do przeciwprostokątnej.

W naszym zadaniu:

Tworzymy odpowiedni stosunek.

Przechodzimy do podstawienia oraz do obliczeń.

(co oczywiście jest błędne)

Odpowiedź: Cos kąta ostrego wynosi i nie wynosi tyle co cosinus 30 stopni.

Wykresem funkcji cosinus jest cosinusoida. Aby ją narysować wskażmy najpierw własności funkcji
1 . znak funkcji cosinus zależy od znaku odciętej, czyli w układzie współrzędnych od osi


2 . dziedziną funkcji jest zbiór liczb rzeczywistych
3 . przeciwdziedziną jest przedział <-1;1> , czyli maksymalna wartość to 1, a minimalna wartość to -1
4 . okresem podstawowym funkcji jest 2 , oznacza to, że funkcja w odstępie 2 ma te same wartości cos (x+2)=cos x
5 . funkcja cosinus jest funkcją parzystą
6 . miejsca zerowe funkcji: /2 + k ;
7 . wartości funkcji cosinus przyjmiemy według poniższej tabeli (wartości odczytane z tablic matematycznych):

8 . aby precyzyjnie narysować cosinusoidę skorzystamy również ze wzorów redukcyjnych, aby móc wyznaczyć wartości większe od podanych powyżej: cos (/2+x)= -sin x oraz cos(+x)= -cos x
Poniżej cosinusoida według powyższych założeń:

Podsumowując więc powyższe rozważania, kąt cosinus 30 stopni znajduje się w pierwszej ćwiartce. Oznacza to, że jego wartość jest dodatnia. Odczytując więc z powyższego wykresu oraz z poniższego układu współrzędnych możemy odczytać, że stosunek liczby pi oraz 6 to nic innego jak cosinus 30 stopni.

Zadanie:
Wyznacz cos kąta w trójkącie równoramiennym o podstawie równej ,kącie wewnętrznym przy podstawie trójkąta oraz kącie przy wierzchołku trójkąta, z którego opada wysokość na podstawę trójkąta. Oblicz wysokość tego trójkąta wiedząc, że oraz że a=4.

Rozwiązanie: najpierw rysujemy rysunek poglądowy:

Zauważ, że wysokość trójkąta równoramiennego dzieli nasz duży trójkąt na 2 trójkąty prostokątne. Zgodnie z zasadami funkcji trygonometrycznych wyznaczamy cos kąta :

Jeśli więc spojrzymy na szary trójkącik to zauważymy, że kąt przy wierzchołku wynosi . Tym samym .

Jeśli więc kąt przy podstawie ma miarę 60°, a kąt przy wierzchołku dużego trójkąta ma miarę 60°, to cały ten trójkąt jest równoboczny. Oznacza to, że a = b = 4.

I sposób rozwiązania zadania

W takim razie korzystając ze wzoru na wysokość trójkąta równobocznego obliczamy wysokość.

II sposób rozwiązania zadania

Drugim sposobem rozwiązania tego zadania będzie zastosowanie twierdzenia Pitagorasa. Spróbuj własnoręcznie na kartce rozpisać sobie to zadanie. Powinna wyjść ci wysokość taka jak mi powyżej.

III sposób rozwiązania zadania

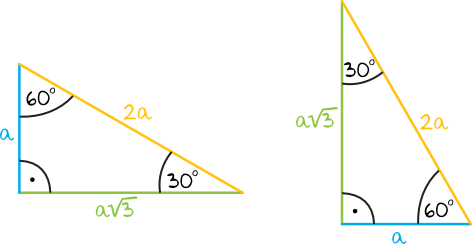
Trzecim sposobem rozwiązania zadania jest zauważenie, że wysokość ta podzieliła trójkąt na dwa „specjalne” trójkąty. Zależności związane z ich bokami przedstawione są poniżej.

My akurat mamy na rysunku dwa trójkąty ustawione tak jak te po prawej. W takim razie bez problemu odczytujemy, że skoro a = 4, to połowa długości naszej podstawy wynosi 2. Mamy tutaj małą kolizję oznaczeń. W każdym razie, każdy z boków na grafice powyżej podzieliłam przez dwa. Dzięki temu bez problemu obliczyłam wysokość. Tym samym h = .

Odpowiedź: Wysokość tego trójkąta to