Cos 60

Zacznijmy od przedstawienia ogólnej definicji cosinusa, bo jest to pełna nazwa skrótu cos.
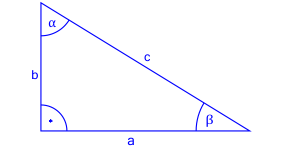
Żebyśmy wiedzieli o co w tej definicji chodzi musimy przypomnieć sobie jak nazywają się poszczególne boki w trójkącie prostokątnym, czyli takim w, którym największy kąt ma miarę 90 stopni.
Dwa boki, które stykają się z kątem prostym, czyli tym o mierze 90 stopni to przyprostokątne, natomiast bok, który leży naprzeciwko tego kąta to przeciwprostokątna.
W trójkącie przeciwprostokątna jest najdłuższa z wszystkich trzech boków.
Przedstawmy te nazwy na rysunku, a następnie przejdziemy do definicji cosinusa.

Znając już jakie nazwy mają poszczególne boki trójkąta możemy przedstawić definicję cosinusa.
Cosinus kąta to stosunek długości przyprostokątnej przylegającej do tego kąta (ta, która styka się z tym kątem) do długości przeciwprostokątnej.
Cosinus kąta jest dodatni tylko dla kątów o mierze od 0 do 90 stopni, a także dla kątów o mierze od 270 do 360 stopni.
Pokażmy na rysunku jak podać cosinus i jego wartość.

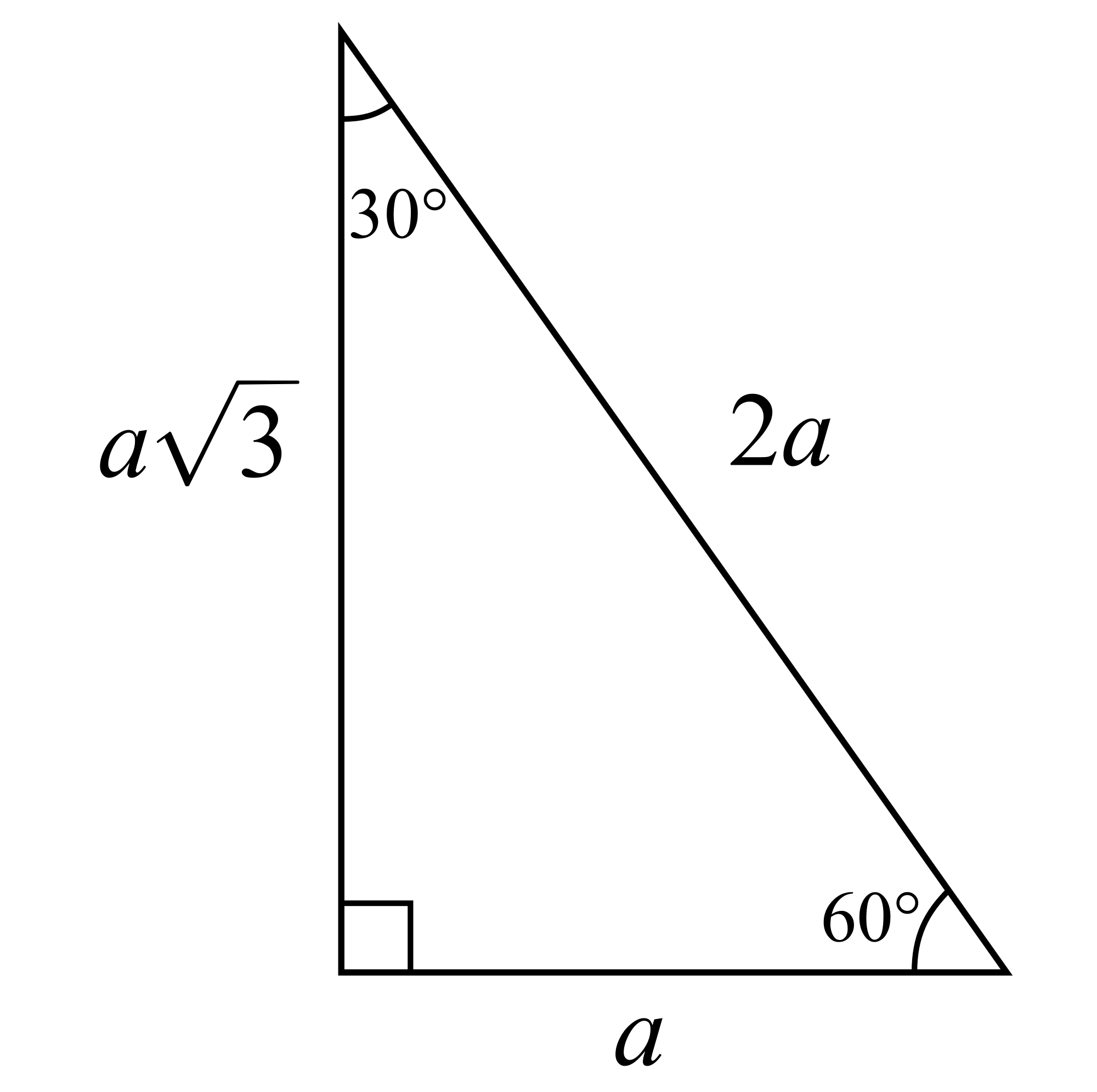
Żeby podać wartość cosinusa kąta o mierze 60 stopni możemy skorzystać z zależności między bokami w trójkącie charakterystycznym, którego kąty mają miary 90, 60 oraz 30.
Najpierw przypomnijmy te zależności.
Naprzeciwko kąta o najmniejszej mierze, czyli kąta 30 stopni leży najkrótszy bok, czyli bok o długości a.
Naprzeciwko kąta o średniej mierze, czyli kąta 60 stopni leży bok o średniej długości, czyli bok .
Naprzeciwko kąta o największej mierze, czyli kąta 90 stopni (kąta prostego) leży najdłuższy bok, czyli bok o długości 2a.
Przedstawmy te zależności na rysunku i korzystając z nich możemy obliczyć wartość cosinusa 60 stopni.


Możemy skrócić literkę „a” i otrzymujemy:

Cosinus 60 stopni jest równy sinusowi 30 stopni.
Podajmy sinus 30 stopni, żeby to udowodnić.
Sinus to stosunek długości przyprostokątnej leżącej naprzeciwko kąta z, którego chcemy wyliczyć sinus do długości przeciwprostokątnej.
Sinus kąta o mierze 30 stopni również możemy obliczyć korzystając z zależności w powyższym trójkącie, czyli 30,60, 90.

Skracamy „a” i zostaje nam:

Zatem:

Zadanie 1.
Korzystając z funkcji trygonometrycznych oraz wiedząc, że przeciwprostokątna w trójkącie prostokątnym ma długość 14, oraz kąt ostry ma miarę 60 stopni oblicz obwód tego trójkąta.

Wiemy, że cosinus, to stosunek długości przyprostokątnej przylegającej do kąta do długości przeciwprostokątnej.
Znamy długość przeciwprostokątnej. Wiemy też ile wynosi cos 60 stopni. Naszą niewiadomą jest zatem przyprostokątna przylegająca do kąta 60 stopni. Możemy więc ułożyć równanie i obliczyć ile wynosi długość tej przyprostokątnej.
Wykonajmy zgodny z treścią zadania rysunek. Przyjmijmy, że „a” oraz „b” to długości przyprostokątnych.

Wiemy, że to
Podstawmy zatem do naszego równania.

Wymnóżmy na krzyż korzystając z proporcji.


Podzielmy obie strony równania przez 2.

Długość „a” możemy obliczyć korzystając z sinusa kąta 60 stopni, ale możemy zrobić innym sposobem żeby z niego nie korzystać.
Wykorzystamy Twierdzenie Pitagorasa.
Przypomnijmy jego treść:
Suma kwadratów przyprostokątnych trójkąta jest równa kwadratowi przeciwprostokątnej tego trójkąta.
Oznaczmy jako „a” i „b” długość przyprostokątnych, a jako „c” długość przeciwprostokątnej.

Wykorzystajmy Twierdzenie Pitagorasa w naszym zadaniu.




Spierwiastkujmy obie strony równania.

Korzystając z umiejętności wyłączania czynnika przed znak pierwiastka zastanówmy się jak można rozpisać liczbę 147.

Długość drugiej przyprostokątnej, to .
Obliczmy teraz obwód tego trójkąta.
Przypomnijmy, że obwód to suma długości wszystkich boków. Zatem naszym zadaniem jest dodać do siebie długości wszystkich boków.



Możemy zostawić to w takiej postaci lub wyłączyć 7 przed nawias: