Działania na kątach skierowanych

Działania na kątach skierowanych
Zacznę od tego czym jest kąt skierowany. Kąt skierowany to dwie półproste, które posiadają wspólny początek. Pierwszą półprostą nazywamy ramieniem początkowym, natomiast drugą ramieniem końcowym tego kąta skierowanego. Kąt skierowany wygląda podobnie do zwykłego kąta, różni się tym, że łuk kąta kończy się strzałką, po to by pokazać, które ramię jest końcowe. Warto zauważyć, że kąt skierowany przeciwny do danego kąta np. 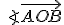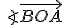do kąta jest kąt z odwróconym wektorem, czyli strzałką, w tym przypadku jest to kąt . Różnią się one tylko kolejnością punktów.
kąt kąt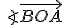

Kąt skierowany ma miarę ujemną, jeśli strzałka przy jego ramieniu jest obrócona zgodnie z ruchem wskazówek zegara, a dodatnią miarę ma, gdy jest ona obrócona przeciwnie do ruchu wskazówek zegara.
Każdą miarę kąta skierowanego można zapisać jako:
n*360° + a, gdzie n jest dowolną liczbą całkowitą, natomiast a nazywamy miarą główną danego kąta skierowanego. Jest to jednocześnie jego najmniejsza nieujemna miara. Miara główna kąta jest zawsze większa lub równa 0° i mniejsza lub równa 360°. Gdy dwa kąty skierowane mają taką samą miarę główną, to są sobie równe.

przykład 1
Oblicz miarę główną kąta skierowanego o mierze:
a) 420° = 1*360° + 60°
a = 60°
b) 1000°= 2*360° + 280°
a = 280°
c) 50°= 0*360° + 50°
a = 50°
d) 2222°= 6*360° + 62°
a = 62°
e) -21°= (-1)*360° + 339°
a = 339°
f) -391°= (-2)*360° + 329°
a = 329°
g) -1590°= (-5)*360° + 210°
a = 210°
h) 1°= 0*360° + 1°
a = 1°
i) 361°= 1*360° + 1°
a = 1°
j) 3601°= 10*360° + 1°
a = 1°