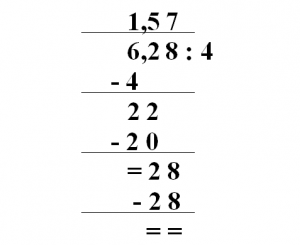Opracowanie:
Dzielenie
Dzielenie
Dzielenie
Dzielenie – działanie pozwalające wyznaczyć iloraz dwóch dowolnych liczb
Działanie te ma swoje elementy składowe:
a (dzielna) : b (dzielnik) = c (iloraz)
np. 8 : 2 = 4
15 : 3 = 5
65 : 5 = 13
2 : 0,5 = 4
18 : 0,25 = 4
Podane wyżej liczby przy dzieleniu przez dany dzielnik dają liczbę całkowitą, jednak może się zdarzyć, że wynik nie będzie liczbą całkowitą. W takiej sytuacji wynik takiego dzielenia można zapisać na różne sposoby:
1 sposób:
np. 8 : 5 = 1 i reszta 3
sprawdzenie 1*5 + 3 = 5 + 3 =8
15 : 4 = 3 i reszta 3
sprawdzenie 3*4 + 3 = 12 + 3 = 15
2 sposób:
np. 8 : 5 = 1,6
15 : 4 = 3,75
Dzielenie pisemne:
Dzielenie małych liczb jest proste i wymaga nauczenia się mnożenia i dzielenia do 100, jednak jeżeli chodzi o większe liczby nie jest to takie łatwe i powszechne, by robić te działanie w pamięci, dlatego korzysta się z kalkulatorów albo stosuje się tak zwane dzielenie pisemne.
By podzielić 475 przez 3 jak na ilustracji powyżej należy:
sprawdzić najpierw ile 3 mieści się w liczbie 4
ze względu, że w 4 mieści się tylko jedna 3, należy zapisać cyfrę 1 nad 4
następnie zapisać wynik mnożenia liczby 3 razy 1 pod 4
jest to 3, więc należy 3 od 4
wynikiem tego jest oczywiście 1 dlatego po 3 robimy kreskę i pod nią zapisujemy 1
następnie patrzymy jaka cyfra jest po 4 w liczbie 475
jest to oczywiście 7, dlatego zapisujemy ją koło 1
sprawdzamy teraz ile wynosi mnożenie 5 i 3
jest to 15, dlatego odejmujemy 15 od 17
robimy kreskę pod 15
wynikiem odejmowania 15 od 17 jest jest 2, więc zapisujemy ją pod kreską
następnie patrzymy jaka cyfra jest następna po 7 w liczbie 475
jest to 5, więc zapisujemy ją koło 2
sprawdzamy ile 3 mieści się w 25
w 25 mieści się osiem 3, więc zapisujemy 8 nad 5
potem mnożymy 8 razy 3
wynikiem jest 24, dlatego zapisujemy tą liczbę pod 25
robimy kreskę
następnie odejmujemy 24 od 25
wynikiem tego odejmowania jest 1
postępowania te należy robić tak długo, aż reszta z odejmowania wyjdzie w końcu 0, jednak nie zawsze tak jest, dlatego liczbę często zaokrągla się do pełnych dziesiątek lub jedności
Tak samo jest z liczbami niecałkowitymi, metoda jest ta sama, tylko zapisujemy przecinek na przecinkiem.
Możliwe jest również dzielenie przez liczby dwucyfrowe, trzycyfrowe oraz większe i zawsze metoda jest taka sama jak w przypadku dzielenia przez cyfry.
Dzielenie ułamków zwykłych polega na mnożeniu pierwszego ułamka oraz odwrotności drugiego, tak jak na przykładzie powyżej.
Istnieją różne zasady pomagające sprawdzić czy dana liczba jest podzielna przez inną:
1 —-> każda liczba jest podzielna przez 1
np. 1, 9, 87, 738, 736484
2 —-> każda liczba parzysta jest podzielna przez 2
np. 2, 4, 6, 8, 10, 28, 756, 75844742
3 —-> każda liczba, której suma cyfr jest podzielna przez 3, jest podzielna przez 3
np. 3, 18, 72, 111111111, 123456789
4 —-> każda liczba, której dwie ostatnie cyfry tworzą liczbę podzielną przez 4, jest podzielna przez 4
np. 4, 28, 512, 45411544 8464647404
5 —-> każda liczba, której liczba jedności wynosi 0 lub 5, jest podzielna przez 5
np. 5, 10, 65, 870, 747465, 5454545645645
6 —-> każda liczba, która jest podzielna przez 2 i 3, jest podzielna przez 6
np. 6, 12, 510, 7818
7 —-> każda liczba, której suma cyfr pomnożona (od prawej) przez kolejne potęgi 3 (włącznie z potęgą zerową: 30=1) dzieli się przez 7, jest podzielna przez 7
np. 7, 21, 616, 10206
8 —-> każda liczba, której trzy ostatnie cyfry tworzą liczbę podzielną przez 8, jest podzielna przez 8
np. 8, 16, 6120, 11048
9 —-> każda liczba, której suma cyfr jest podzielna przez 9, jest podzielna przez 9
np. 9, 909, 1221354, 987654321
10 —-> każda liczba, której cyfra jedności wynosi 0, jest podzielna przez 10
np. 10, 170, 16370, 3634646360