Opracowanie:
Figury przestrzenne
Figury przestrzenne
Figury przestrzenne zwane inaczej bryłami lub figurami trójwymiarowymi to figury geometryczne mające długość, szerokość i wysokość (dla porównania figury geometryczne płaskie posiadają tylko długość i szerokość).
Przykłady figur przestrzennych:
Graniastosłup

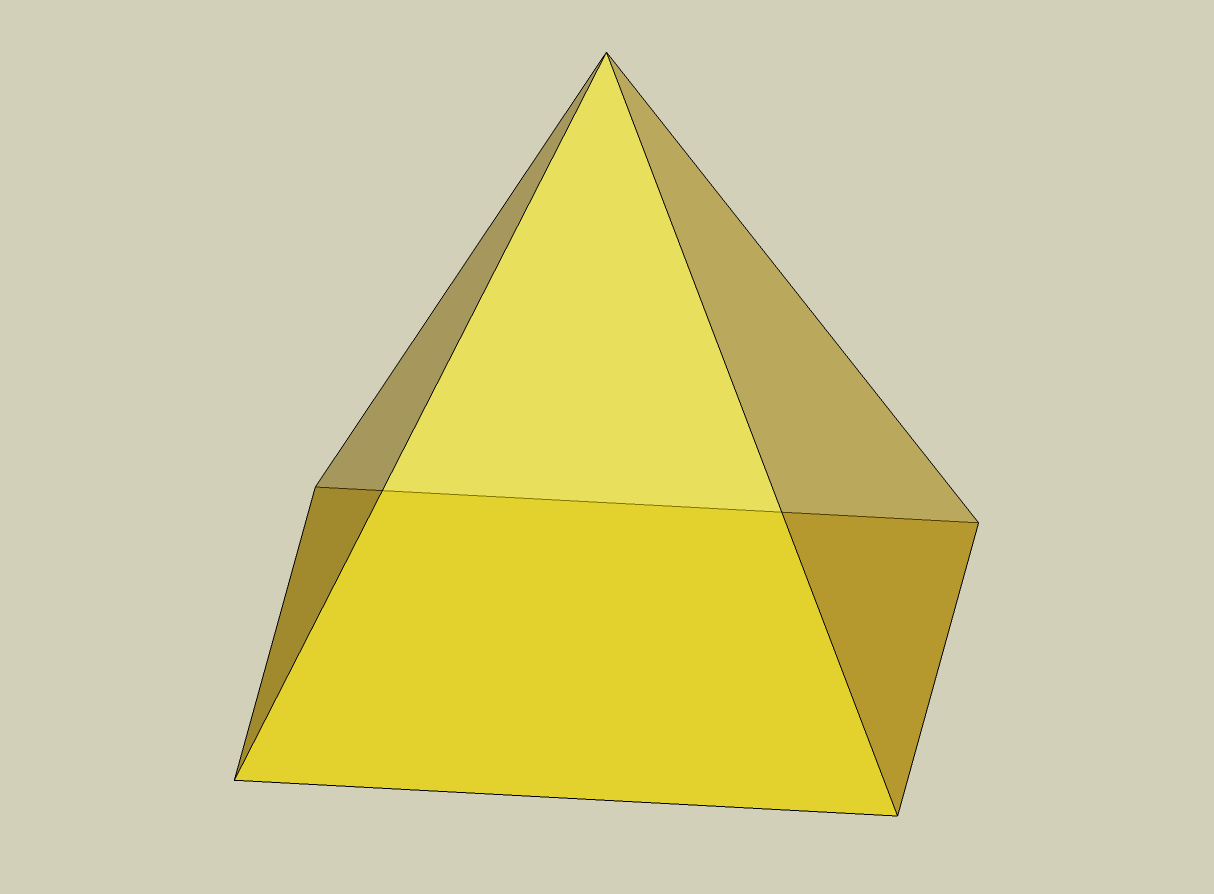
Ostrosłup
Ostrosłup to wielościan mający jedną podstawę, a wszystkie jego ściany boczne spotykają
się w jednym miejscu. To miejsce nazywamy wierzchołkiem. Podstawa w ostrosłupie
podobnie jak w graniastosłupie może być dowolnym wielokątem, a jeżeli jest to wielokąt
foremny to mówimy, że ostrosłup jest prawidłowy. Na rysunku obok znajduje się ostrosłup
prawidłowy czworokątny.
Kula
Kula należy do brył obrotowych. Powstaje podczas obracania dowolnego koła wokół jego
średnicy. Kulę można również opisać jako część przestrzeni, która jest ograniczona sferą.
Po prawej strony został pokazany przykład kuli.
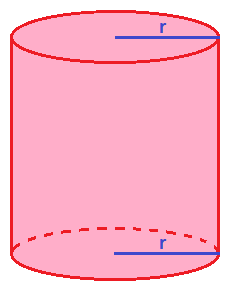
Walec
Walec podobnie jak kula należy do brył obrotowych. Powstaje podczas obracania prostokąta
wokół jednego z boków. Walec także jest bryłą, która jest ograniczona powierzchnią walcową
i dwiema płaszczyznami, które są nierównoległe do jej tworzącej. Podstawą tej bryły zawsze
jest koło. Przykład walce jest pokazany po prawej stronie.
Stożek
Stożek należy do brył obrotowych. Powstaje podczas obrotu trójkąta prostokątnego wokół
jednej z przyprostokątnych. Ta przyprostokątna staje się wysokością stożka, a druga
przyprostokątna jego promieniem podstawy. Podstawą bryły jest koło.
Tabela przedstawiająca wzory na pole powierzchni całkowitej oraz objętość ww. figur przestrzennych
nazwa figury przestrzennej