Figury przystające

Figury przystające to takie 2 lub więcej figur, które są do siebie podobne pod względem długości boków i miar kątów.

W każdym wielokącie są tylko 2 cechy przystawania ( w przypadku trójkątów są aż 3):

a) w trójkącie:
bok-bok-bok (bbb)- trójkąty mają te same długości boków
bok-kąt-bok (bkb)- trójkąty mają zawarty ten sam kąt pomiędzy dwoma takimi samymi bokami
kąt-bok-kąt (kbk)- trójkąty mają 2 identyczne kąty przy jednym boku
b) w czworokątach:
bok-kąt-bok-kąt-bok (bkbkb)- czworokąty mają 2 takie same kąty zawarte pomiędzy 3 bokami.
kąt-bok-kąt-bok-kąt (kbkbk)- czworokąty mają 3 takie same kąty przy 2 takich samych bokach.

Cechy przystawanie w wielokątach o większej ilości bokach, są dłuższe, ale w różnorakich zadaniach mamy stwierdzić, że częściej występują zadania o przystawaniu trójkątów i czworokątów, a jeśli są inne wielokąty, to po kolei porównujemy te same boki (pamiętając, że jeśli figury są odwrócone, to w myślach obracamy figurę) i kąty

Zad. 1
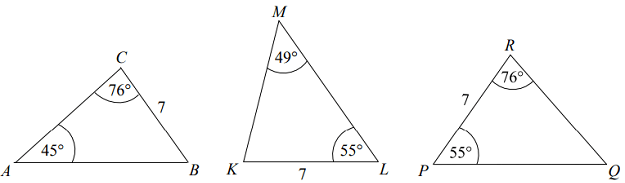
które trójkąty na rysunku powyżej są przystające?

Wskazówka:
zanim rozwiążesz zadanie, przeanalizuj rysunek (jeśli go nie ma, naszkicuj sobie) i znajdź informacje, których Ci brakuje, by jednoznacznie stwierdzić o przystawaniu wielokątów (pamiętając o cechach przystawania)

kąty trójkąta ABC- 45°, 76°, α=59°
kąty trójkąta KLM- 55°, 49°, β= 76°
kąty trójkąta PRQ- 55°, 76°, ƍ= 49°

Niestety nie mamy wszystkich informacji (nie mamy jednego kąta przy boku 7)
α= 180°- (45°+76°)= 180°-121°=59°
β= 180°- (55°+49°)= 180°-104°= 76°
ƍ=180°- (55°+76°)= 180°-131°= 49°

Teraz możemy podać odpowiedź, bo widzimy brakujące kąty i ich położenie, więc
Odp.: przystające są trójkąty KLM i PRQ , gdyż przy boku 7 są zawarte odpowiednio równe kąty (55° i 76°), czyli z cechy kbk

Zad. 2

Dane są 2 prostokąty, jeden z nich ma boki długości 3 i 4, gdy drogi ma jeden bok długości 3 i przekątną długości 5. Czy prostokąty są przystające?

Pierwszy prostokąt nazwijmy ABCD, a drugi EFGH
boki prostokąta ABCD- 3 i 4
bok prostokąta EFGH- 3 i ,b= 4′ , przekątna- 5

z takich danych, nie możemy jednoznacznie stwierdzić czy prostokąty są przystające (brakuje nam drugiego boku w prostokącie EFGH), ale możemy wykorzystać fakt, że przekątna prostokąta dzieli go na 2 przystające trójkąty prostokątne, a więc brakujący bok obliczymy z twierdzenia pitagorasa (pamiętając o przekształceniu)

c2= a2 + b2 /- a2
b2= c2 – a2
b2= 52 – 32
b2= 25 – 9
b2= 16 /
b= 4
Teraz możemy dać odpowiedź

Odp,: prostokąty są przystające (z cechy bkbkb)