Funkcja rosnąca

Mówimy, że funkcja rośnie (jest rosnąca) w przedziale dziedziny jeśli zachodzi warunek:
Gdy < to < .

W przypadku funkcji liniowej można to uprościć.
Funkcja liniowa f(x) = ax + b jest rosnąca jeżeli jej współczynnik kierunkowy a > 0.
Aby obliczyć współczynnik kierunkowy należy wybrać z wykresu 2 punkty, np. A(), B. Jeżeli mamy 2 punkty to współczynnik kierunkowy .

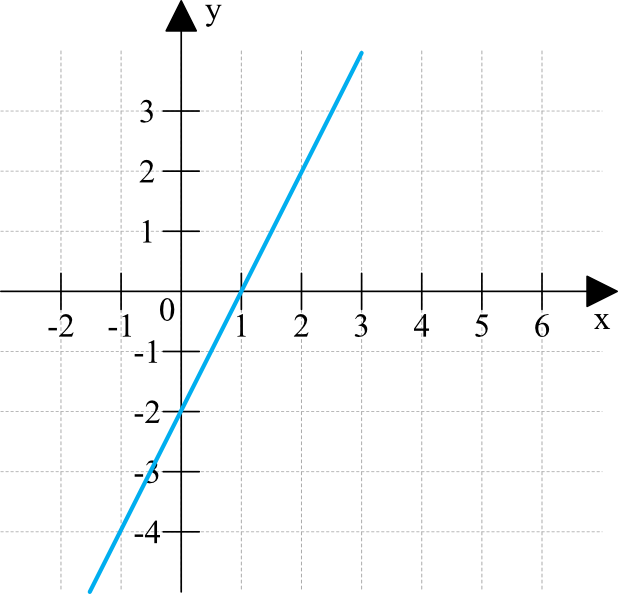
Przykłady wykresów funkcji rosnących:

ZADANIA:

ZADANIE 1
Wykaż, że funkcja f(x) = jest rosnąca.

Współczynnik kierunkowy a > 0, zatem podana funkcja jest rosnąca . Spróbujemy jednak rozwiązać to zadanie opierając się o definicję funkcji rosnącej.

< < < 0 < 0 =
=

= = < 0 2 > 0, < 0, Odp. Funkcja jest rosnąca, ponieważ < 0 . ZADANIE 2
Funkcja przechodzi przez A(-1, 2), B(2, 3). Wykaż, że funkcja przechodząca przez podane punkty jest funkcją rosnącą.

=

Odp. Podana funkcja jest funkcją rosnącą, ponieważ współczynnik kierunkowy a > 0.