Funkcje hiperboliczne

Funkcje hiperboliczne mają wiele wspólnego z funkcjami trygonometrycznymi. Przy użyciu funkcji mogą powstać różne „wariacje”, które stają się funkcjami hiperbolicznymi.

Wyróżniamy cztery funkcje hiperboliczne. Zauważ, że do nazw trygonometrycznych dodajemy wyraz „hiperboliczny”, a do skrótu dodajemy literę „h” na koniec.

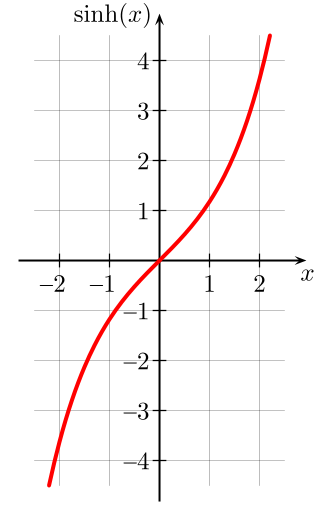
Sinus hiperboliczny —>
Cosinus hiperboliczny —>
Tangens hiperboliczny —>
Cotangens hiperboliczny —>

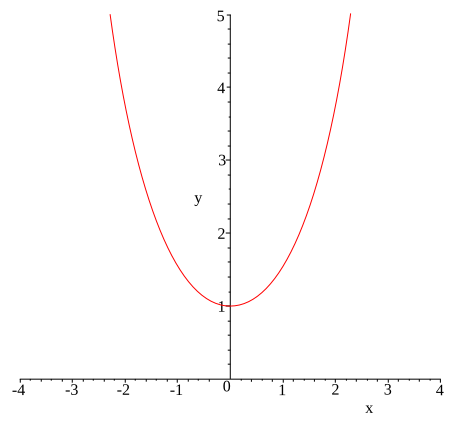
Krzywa łańcuchowa stanowi wykres cosinusa hiperbolicznego.

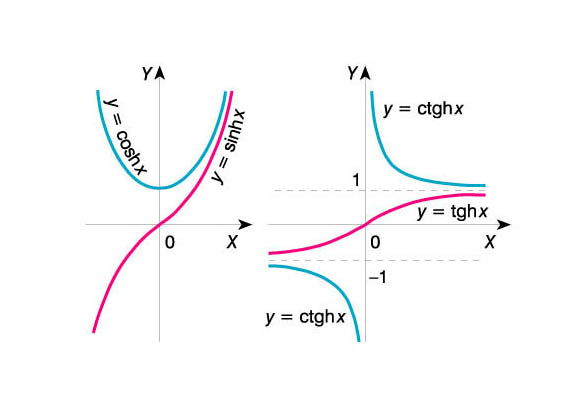
Na powyższym wykresie jest porównanie trzech wykresów funkcji hiperbolicznych.

Wzory przydatne podczas rozwiązywania zadań z takimi funkcjami

Przede wszystkim warto wspomnieć o zachodzących równościach:




Oczywiście, każde z tych zależności możemy udowadniać, a więc wystarczyłoby podstawić pod prawą stronę równania dane wyróżnione powyżej, a następnie uzyskalibyśmy te same wartości co po lewej stronie równania.

Zastosowanie funkcji hiperbolicznych

Przede wszystkim możemy się spotkać z funkcjami hiperbolicznymi podczas korzystania ze wzoru elementarnego dla całek nieoznaczonych. Ten wzór wygląda następująco:

Funkcje hiperboliczne a pochodne
W tym zagadnieniu trygonometryczne jak i hiperboliczne funkcje praktycznie się pokrywają.

(inny znak niż w trygonometrii)

Podsumowując więc, funkcje trygonometryczne są podobne do siebie pod względem nazw, własności oraz pochodnych.