Opracowanie:
Funkcje trygonometryczne

Funkcje trygonometryczne

Zweryfikowane

Zapraszam na szczegółowe omówienie wszystkich funkcji trygonometrycznych.

Do funkcji trygonometrycznych zaliczamy funkcje: sinus, cosinus, tangens, cotangens oraz obecnie rzadziej używane secans i cosecans.
Na początku omówimy sobie własności każdej funkcji, wykres, dziedzinę i przeciwdziedzinę, funkcje odwrotne, parzystość, monotoniczność itd., a następnie przejdziemy do zależności między tymi funkcjami i przykładów ich użycia.

Przydatne informacje:
> funkcje trygonometryczne są ciągłe i różniczkowalne w swoich dziedzinach (zaliczamy je do funkcji elementarnych)
> funkcje trygonometryczne nie są odwracalne, bo nie są różniczkowalne. Funkcje odwrotne można określić tylko w pewnych przedziałach.

Sinus
W obliczeniach matematycznych stosujemy zapis , co oznacza wartość funkcji sinus dla kąta
Wykres funkcji sinus nazywamy sinusoidą.

Jak widać na wykresie sinus jest funkcją okresową (z okresem równym ) oraz NIEPARZYSTĄ (oznacza to, że ).

Dziedzina funkcji sinus to (Zbiór liczb rzeczywistych)
Zbiór wartości (przeciwdziedzina) to (Przedział domknięty od -1 do 1)

Sinus przyjmuje swoją maksymalną wartość 1 w punktach , a minimalną wartość -1 w punktach (gdzie k to liczba całkowita)
Miejsca zerowe funkcji sinus to punkty (gdzie k to liczba całkowita)

Monotoniczność: Funkcja sinus jest monotoniczna tylko przedziałami.

Funkcja odwrotna do sinus to arcus sinus. Poniżej przedstawiam proces tworzenia wykresu funkcji arcus sinus. Jak już wspomniałam funkcje trygonometryczne są różnowartościowe tylko na pewnych odcinkach. Wybieramy zatem z dziedziny funkcji odcinek, na którym jest ona różnowartościowa i dopiero odbijamy względem prostej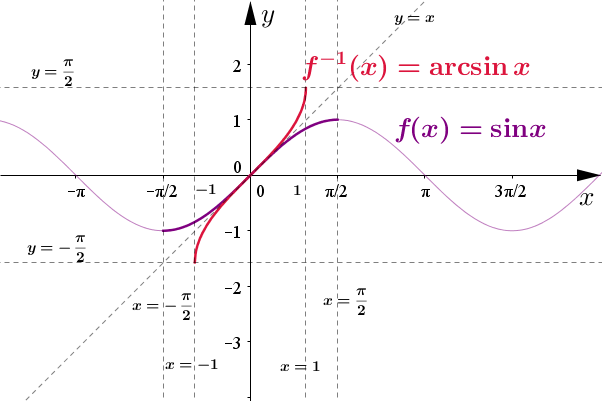

Dziedzina funkcji arcus sinus to (Przedział domknięty od -1 do 1)
Zbiór wartości (przeciwdziedzina) funkcji arcus sinus to (Przedział domknięty od do )

Pochodna funkcji sinus
${displaystyle sin 'x=cos x=sin left({tfrac {pi }{2}}+xright)}$

Całka funkcji sinus

Cosinus
W obliczeniach matematycznych stosujemy zapis , co oznacza wartość funkcji cosinus dla kąta
Wykres funkcji sinus nazywamy cosinusoidą.

Jak widać na wykresie cosinus jest funkcją okresową (z okresem równym ) oraz PARZYSTĄ (oznacza to, że ).

Ciekawostka.
Cosinusoida jest przesuniętą sinusoidą o wektor

Dziedzina funkcji cosinus to (Zbiór liczb rzeczywistych)
Zbiór wartości (przeciwdziedzina) to (Przedział domknięty od -1 do 1)

Monotoniczność: Funkcja cosinus jest monotoniczna tylko przedziałami.

Cosinus przyjmuje swoją maksymalną wartość 1 w punktach , a minimalną wartość -1 w punktach (gdzie k to liczba całkowita)
Miejsca zerowe funkcji cosinus to punkty (gdzie k to liczba całkowita)

Funkcja odwrotna do cosinus to arcus cosinus. Poniżej przedstawiam proces tworzenia wykresu funkcji arcus cosinus. Jak już wspomniałam funkcje trygonometryczne są różnowartościowe tylko na pewnych odcinkach. Wybieramy zatem z dziedziny funkcji odcinek, na którym jest ona różnowartościowa i dopiero odbijamy względem prostej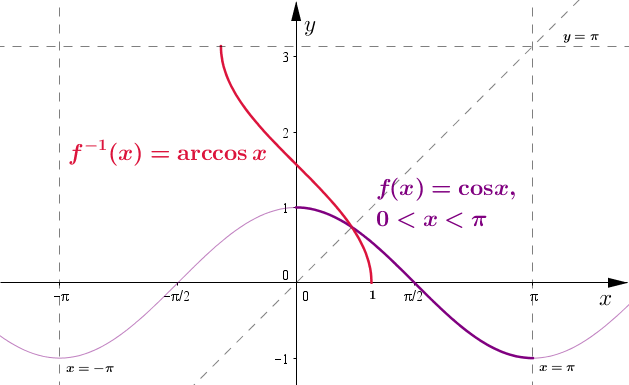

Dziedzina funkcji arcus cosinus to (Przedział domknięty od -1 do 1)
Zbiór wartości (przeciwdziedzina) funkcji arcus cosinus to

Pochodna funkcji cosinus
${displaystyle cos 'x=-sin x=cos left({tfrac {pi }{2}}+xright)}$

Całka funkcji cosinus
Tangens
W obliczeniach matematycznych stosujemy zapis lub , co oznacza wartość funkcji tangens dla kąta
Wykres funkcji sinus nazywamy tangensoidą.

Jak widać na wykresie tangens jest funkcją okresową (z okresem równym ) oraz NIEPARZYSTĄ (oznacza to, że ).
Asymptoty pionowe ma w punktach

Dziedzina funkcji tangens to (Zbiór liczb rzeczywistych z wyłączeniem asymptot pionowych)
Zbiór wartości (przeciwdziedzina) to (Zbiór liczb rzeczywistych)

Monotoniczność: Funkcja tangens jest rosnąca w przedziałach

Tangens nie przyjmuje wartości maksymalnej, ani minimalnej.
Miejsca zerowe funkcji tangens to punkty (gdzie k to liczba całkowita)

Funkcja odwrotna do tangens to arcus tangens. Poniżej przedstawiam proces tworzenia wykresu funkcji arcus tangens. Jak już wspomniałam funkcje trygonometryczne są różnowartościowe tylko na pewnych odcinkach. Wybieramy zatem z dziedziny funkcji odcinek, na którym jest ona różnowartościowa i dopiero odbijamy względem prostej y=x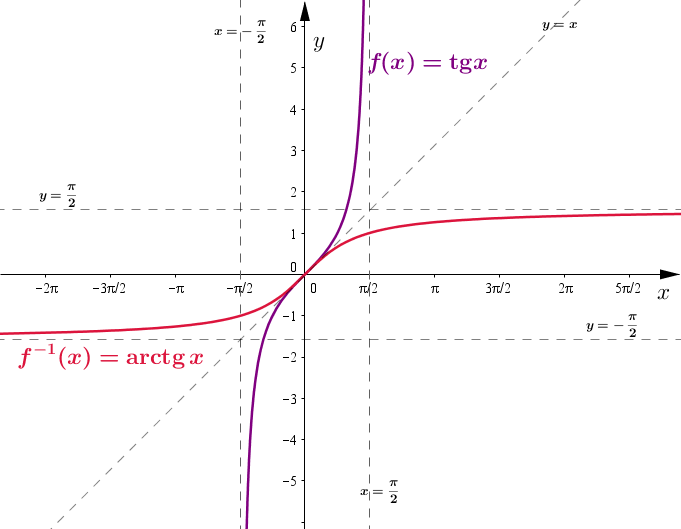

Dziedzina funkcji arcus tangens to (Zbiór liczb rzeczywistych)
Zbiór wartości (przeciwdziedzina) funkcji arcus tangens to (Przedział domknięty od do )

Pochodna funkcji tangens
${displaystyle operatorname {tg} 'x={tfrac {1}{cos ^{2}x}}=sec ^{2}x=1+operatorname {tg} ^{2}x{mbox{ dla }}xneq {tfrac {pi }{2}}+kpi ,kin mathbb {Z} }$

Całka funkcji tangens

Cotangens
W obliczeniach matematycznych stosujemy zapis lub , co oznacza wartość funkcji cotangens dla kąta
Wykres funkcji sinus nazywamy cotangensoidą.

Jak widać na wykresie cotangens jest funkcją okresową (z okresem równym ) oraz NIEPARZYSTĄ (oznacza to, że ).
Asymptoty pionowe ma w punktach

Dziedzina funkcji cotangens to (Zbiór liczb rzeczywistych z wyłączeniem asymptot pionowych)
Zbiór wartości (przeciwdziedzina) to (Zbiór liczb rzeczywistych)

Monotoniczność: Funkcja cotangens jest malejąca w przedziałach

Tak samo jak funkcja tangens, cotangens nie przyjmuje wartości maksymalnej, ani minimalnej.
Miejsca zerowe funkcji cosinus to punkty (gdzie k to liczba całkowita)

Funkcja odwrotna do cotangens to arcus cotangens. Poniżej przedstawiam proces tworzenia wykresu funkcji arcus cotangens. Jak już wspomniałam funkcje trygonometryczne są różnowartościowe tylko na pewnych odcinkach. Wybieramy zatem z dziedziny funkcji odcinek, na którym jest ona różnowartościowa i dopiero odbijamy względem prostej y=x

Dziedzina funkcji arcus cotangens to (Zbiór liczb rzeczywistych)
Zbiór wartości (przeciwdziedzina) funkcji arcus secans to (Przedział domknięty od 0 do )

Pochodna funkcji cotangens ${displaystyle operatorname {ctg} 'x=-{tfrac {1}{sin ^{2}x}}=-operatorname {cosec} ^{2}x=-(1+operatorname {ctg} ^{2}x){mbox{ dla }}xneq kpi ,kin mathbb {Z} }$
Całka funkcji cotangens

Secans jest to funkcja trygonometryczna, odwrotność cosinusa (nie mylić z arcus cosinus!!!)
Secans jest odwrotnością cosinusa w sensie arytmetycznym (podczas gdy funkcja arcus cosinus jest funkcją odwrotną funkcji cosinus)

Wykres funkcji secans:

Jak widać na wykresie secans jest funkcją okresową (z okresem równym ) oraz PARZYSTĄ (oznacza to, że ).
Asymptoty pionowe ma w punktach

Dziedzina funkcji secans to (Zbiór liczb rzeczywistych z wyłączeniem asymptot pionowych)
Zbiór wartości (przeciwdziedzina) to (Zbiór liczb rzeczywistych z wyłączeniem przedziału otwartego od -1 do 1 )

Funkcja secans nie ma miejsc zerowych oraz nie przyjmuje wartości maksymalnej i minimalnej.

Funkcja odwrotna do secans to arcus secans. Poniżej przedstawiam w jaki sposób tworzymy wykres funkcji arcus secans. Jak już wspomniałam funkcje trygonometryczne są różnowartościowe tylko na pewnych odcinkach. Wybieramy zatem z dziedziny funkcji odcinek, na którym jest ona różnowartościowa.

Dziedzina funkcji arcus secans to (Zbiór liczb rzeczywistych z wyłączeniem przedziału otwartego od -1 do 1)
Zbiór wartości (przeciwdziedzina) funkcji arcus secans to (Przedział domknięty od 0 do z wyłączeniem )

Pochodna funkcji secans

Całka funkcji secans , gdzie

Cosecans jest to funkcja trygonometryczna, odwrotność sinusa (nie mylić z arcus sinus!!!)
Cosecans jest odwrotnością sinusa w sensie arytmetycznym (podczas gdy funkcja arcus sinus jest funkcją odwrotną! funkcji sinus)

Wykres funkcji cosecans:

Jak widać na wykresie cosecans jest funkcją okresową (z okresem równym ) oraz NIEPARZYSTĄ (oznacza to, że ).
Asymptoty pionowe ma w punktach

Dziedziną funkcji cosecans jest (Zbiór liczb rzeczywistych z wyłączeniem asymptot pionowych)
Zbiór wartości (przeciwdziedzina) to (Zbiór liczb rzeczywistych z wyłączeniem przedziału otwartego od -1 do 1 )

Funkcja cosecans nie ma miejsc zerowych oraz nie przyjmuje wartości maksymalnej i minimalnej.

Funkcja odwrotna do cosecans to arcus cosecans. Poniżej przedstawiam wykres funkcji arcus cosecans. Proces tworzenia wykresu jest analogiczny do procesu tworzenia wykresu funkcji arcus secans.

Dziedzina funkcji arcus cosecans to (Zbiór liczb rzeczywistych z wyłączeniem przedziału otwartego od -1 do 1 )
Zbiór wartości (przeciwdziedzina) funkcji arcus cosecans to (Przedział domknięty od do z wyłączeniem 0)

Zależność funkcji cosecans od secans:

Pochodna funkcji cosecans

Całka funkcji cosecans

Wartości funkcji trygonometrycznych dla kątów 0°, 15°, 30°, 45°, 60°, 75°, 90°

radiany

stopnie

15o

30o

45o

60o

75o

90o

sinus

${displaystyle {tfrac {{sqrt {6}}-{sqrt {2}}}{4}}}$

$tfrac{1}{2}$

${displaystyle {tfrac {sqrt {2}}{2}}}$

${displaystyle {tfrac {sqrt {3}}{2}}}$

${displaystyle {tfrac {{sqrt {6}}+{sqrt {2}}}{4}}}$

cosinus

${displaystyle {tfrac {{sqrt {6}}+{sqrt {2}}}{4}}}$

${displaystyle {tfrac {sqrt {3}}{2}}}$

${displaystyle {tfrac {sqrt {2}}{2}}}$

$tfrac{1}{2}$

${displaystyle {tfrac {{sqrt {6}}-{sqrt {2}}}{4}}}$

tangens

${displaystyle {tfrac {sqrt {3}}{3}}}$

nieokreślony

cotangens

nieokreślony

${displaystyle {tfrac {sqrt {3}}{3}}}$

secans

${displaystyle {tfrac {2{sqrt {3}}}{3}}}$

nieokreślony

cosecans

nieokreślony

${displaystyle {tfrac {2{sqrt {3}}}{3}}}$

WZORY REDUKCYJNE
Najpierw zobaczmy w jaki sposób numerujemy ćwiartki w układzie współrzędnych.

I ĆWIARTKA

II ĆWIARTKA

III ĆWIARTKA

IV ĆWIARTKA

90o

180o

270o

360o

{displaystyle operatorname {cosec} {alpha }}

{displaystyle operatorname {cosec} {phi }}

W jaki sposób zapamiętać tą tabelkę? Czy to jest możliwe??
Przedstawiam Ci rymowankę, która ma zaledwie 4 wersy, a pomoże Ci zapamiętać, gdzie minusy, a gdzie plusy dla funkcji sinus, cosinus, tangens i cotangens.

W pierwszej wszystkie są dodatnie,
W drugiej TYLKO sinus,
W trzeciej tangens i cotangens,
A w czwartej cosinus.

Tożsamości trygonometryczne, które przydadzą Ci się przy rozwiązywaniu różnych zadań matematycznych, na każdym poziomie nauki:

1) jedynka trygonometryczna

2) tangens i cotangens za pomocą sinusa i cosinusa
${displaystyle {begin{aligned}operatorname {tg} alpha &={tfrac {sin alpha }{cos alpha }},;alpha neq {tfrac {pi }{2}}+kpi \operatorname {ctg} alpha &={tfrac {cos alpha }{sin alpha }},;alpha neq kpi end{aligned}},quad kin mathbb {Z} .}$

3) suma i różnica kątów

4) suma i różnica sinusa i cosinusa
${displaystyle sin alpha pm sin beta =2sin {tfrac {alpha pm beta }{2}}cdot cos {tfrac {alpha mp beta }{2}}}$
${displaystyle cos alpha +cos beta =2cos {tfrac {alpha +beta }{2}}cdot cos {tfrac {alpha -beta }{2}}}$
${displaystyle cos alpha -cos beta =-2sin {tfrac {alpha +beta }{2}}cdot sin {tfrac {alpha -beta }{2}}}$

5) sinus i cosinus podwójnego kąta

6) iloczyn
$cos alpha cdot cos beta ={tfrac {cos(alpha -beta )+cos(alpha +beta )}2}$
$sin alpha cdot sin beta ={tfrac {cos(alpha -beta )-cos(alpha +beta )}2}$
$sin alpha cdot cos beta ={tfrac {sin(alpha -beta )+sin(alpha +beta )}2}$

Funkcje trygonometryczne możemy wyrazić jako stosunki długości boków trójkąta prostokątnego. A mianowicie:

kąt prosty to oczywiście kąt ACB

jest to stosunek długości przyprostokątnej a leżącej naprzeciw kąta do długości przeciwprostokątnej c, a zatem

jest to stosunek długości przyprostokątnej b leżącej przy kącie do długości przeciwprostokątnej c, a zatem

jest to stosunek długości przyprostokątnej a leżącej naprzeciw kąta do długości przyprostokątnej a, a zatem

jest to stosunek długości przyprostokątnej b leżącej przy kącie do długości przyprostokątnej a, a zatem (zauważmy, że będzie to samo co )

jest to stosunek długości przeciwprostokątnej c do długości przyprostokątnej b leżącej przy kącie , a zatem (zauważmy, że będzie to samo co )

jest to stosunek długości przeciwprostokątnej c do długości przyprostokątnej a leżącej naprzeciw kąta , a zatem (zauważmy, że będzie to samo co )

Zadanie 1. Rozwiąż równanie:

Rozwiązanie:
Skorzystamy z jedynki trygonometrycznej:

Obserwuj uważnie kolejne przejścia.
Najpierw z jedynki trygonometrycznej dokonujemy podstawienia

Wymnażamy nawiasy.

Przenosimy wszystko na lewą stronę.

Teraz czas na sprytne przejście. Z dwóch pierwszych składników wyciągniemy przed nawias, a z dwóch ostatnich wyciągniemy -1/

i wyciągamy powstałą część wspólną z obu składników.

Zatem
lub

Pozostało dopasować wartości x.
Odpowiedź:
,
,

Powyższe zadanie zostało zweryfikowane przez nauczyciela

Opracowanie: Funkcje trygonometryczne

Funkcje trygonometryczne

Opracowanie:
Funkcje trygonometryczne