Opracowanie:
Odcinki w układzie współrzędnych
Odcinki w układzie współrzędnych
W układzie współrzędnych „jedna kreseczka” na osiach liczbowych może mieć różną wartość. Na jednej osi współrzędnych może wynosić 1, natomiast na innym może wynosić 5. Wszystko zależy od jednostki jaką przyjmiemy.
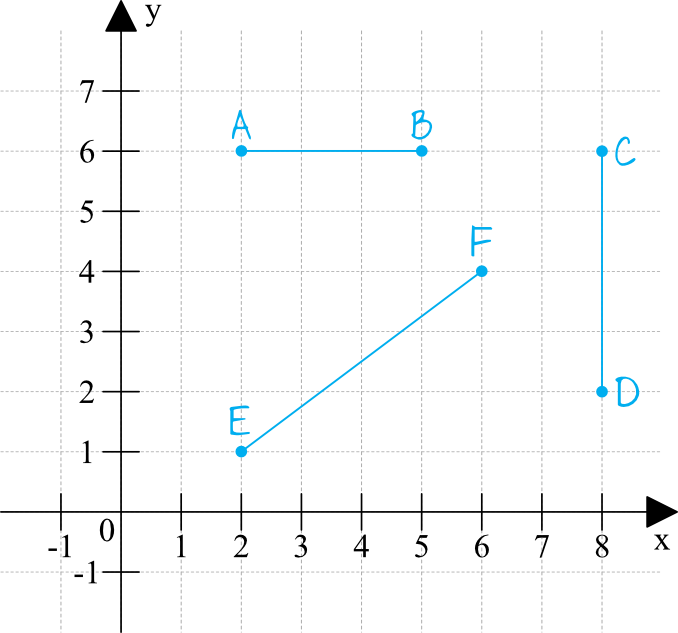
W układzie współrzędnych mogą być zaznaczane odcinki. Mogą one leżeć równolegle do osi, czyli po kratkach, ale mogą także leżeć na ukos.
Patrzymy na jednostki. Jedna kratka to 1.
W układzie współrzędnych możemy obliczać długości odcinków, a nawet ich środek.
Gdy odcinek jest położony równolegle do kratek, wtedy nie mamy problemu żeby podać jego długość, bo wystarczy policzyć jedynie kratki. Jednak gdy odcinek jest położony po skosie tak jak w przypadku odcinka |EF| możemy mieć już problem z podaniem jego długości, a co dopiero środka.
Długość odcinka wyraża się wzorem:
Dla przykładu obliczmy długość odcinka |EF|.
Najpierw musimy podać współrzędne punktu E oraz punktu F.
Pierwiastkujemy.
Zatem długość odcinka to 5.
Podajmy również wzór na środek odcinka i również wyznaczmy środek odcinka |EF|.
W naszym przypadku małe literki A i B zmieniają się na E i F.