Parabola

Czym jest parabola?
Parabola to wykres funkcji kwadratowej.
Przypomnijmy w takim razie informacje o funkcji kwadratowej.
Ogólny wzór funkcji kwadratowej to .

„a” to współczynnik kierunkowy funkcji. W przypadku funkcji kwadratowej „a” nie może równać się „0”, ponieważ otrzymujemy wtedy wzór funkcji liniowej ().

Jak wygląda parabola, od czego zależy jej położenie, skąd wiemy gdzie jest wierzchołek paraboli? W tym opracowaniu postaram się to wszystko Wam rozjaśnić.

Najpierw omówmy czym jest parabola, a następnie pokaże Wam dwa rodzaje wykresu paraboli i wyjaśnię w jakich przypadkach, który z nich stosujemy.

Każda parabola ma wierzchołek. W sytuacji przedstawionej na naszym rysunku, który zamieszczony jest powyżej wierzchołek znajduje się w punkcie P(0,0).

Parabola ma również dwa ramiona. Są one symetrycznie od siebie oddalone. Co to oznacza?
Jeżeli punkt położony na wysokości 4 (patrzymy na oś Y) po prawej stronie współrzędną „x” ma równą 2, to po lewej stronie będzie -2. (W jednakowej odległości od wierzchołka).
Oś symetrii przechodzi przez wierzchołek paraboli.

Ramiona paraboli mogą być skierowane w górę lub w dół.
Porównajmy oba te przypadki.

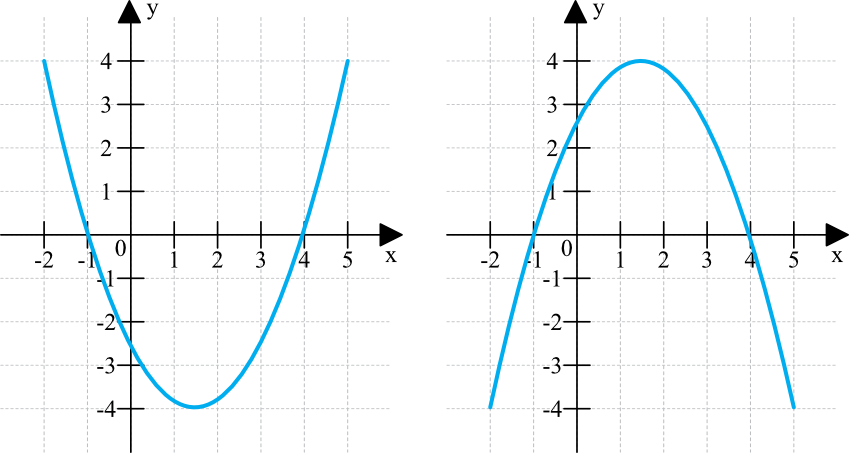
Na pierwszym rysunku: Na drugim rysunku:
Ramiona paraboli skierowane w górę. 1. Ramiona paraboli skierowane w dół.
Oznacza to, że współczynnik „a” jest dodatni. 2. Oznacza to, że współczynnik kierunkowy „a” jest ujemny.
Wierzchołek znajduje się w punkcie P(1,5;-4). 3. Wierzchołek znajduje się w punkcie P(1,5;4).

Wniosek:
Gdy a>0, ramiona paraboli skierowane są w górę.
Gdy a<0, ramiona paraboli skierowane są w dół.

Jak narysować parabolę?
Po pierwsze musimy ustalić czy ramiona będą skierowane w górę czy w dół. Czyli sprawdzamy czy współczynnik znajdujący się przy x2, czyli współczynnik kierunkowy „a” jest większy od 0, czy mniejszy od 0.
Jeśli większy to ramiona paraboli będą skierowane w górę, jeśli mniejszy to ramiona paraboli będą skierowane w dół.
Jeśli będzie równy „0”, wtedy nie jest to funkcja kwadratowa, a funkcja liniowa, czyli prosta linia w odróżnieniu od paraboli nieposiadająca ramion i nieposiadająca wierzchołka.
Następnie obliczamy w jakim punkcie znajduje się wierzchołek paraboli.
Musimy tutaj wprowadzić potrzebne wzory.
Zakładamy, że wierzchołek paraboli ma współrzędne: W(p;q).
Podajmy zatem wzór jak obliczyć p=. Q natomiast obliczymy podstawiają pod wzór funkcji pod „x” wartość, która nam wyszła w p. Czyli . Istnieje także drugi sposób. Korzystając z niego musimy znać wzór na deltę: Δ.
Wzór na współrzędną „q” wierzchołka paraboli, to .
Następnie o ile istnieją obliczamy miejsca zerowe tej funkcji.
Czym w ogóle są miejsca zerowe?
Miejsca zerowe (inaczej pierwiastki funkcji) to punkty w, których wykres funkcji przecina oś X.
Przykładowe współrzędne miejsc zerowych to (4,0); (-9,0); (-11,0).
Żeby obliczyć miejsca zerowe funkcji kwadratowej musimy obliczyć deltę, o której już wcześniej wspominałam.
.
W zależności od wartości delty ustalimy czy funkcja kwadratowa ma miejsca zerowe, czy ich nie ma, a także jeśli są to jakie i ile ich jest.
Przedstawmy pewne reguły, skąd wiedzieć czy są miejsca zerowe.
Gdy Δ>0, funkcja kwadratowa ma dwa miejsca zerowe.
Gdy Δ<0, funkcja kwadratowa nie ma miejsc zerowych.
Gdy Δ=0, funkcja kwadratowa ma jedno podwójne miejsce zerowe.
Przećwiczmy teraz obliczanie delty i ustalanie czy funkcja kwadratowa ma miejsca zerowe, czy ich nie ma, a jeśli ma to ile ich jest.

Ćwiczenie 1
Sprawdź, czy funkcja kwadratowa ma miejsca zerowe.

a) y= 7x2+5x+2
Na początku wypiszmy współczynniki tej funkcji:
a=7 b=5 c=2
Podstawmy liczby pod wzór na deltę.
Δ=b2-4ac=(5)2-4*(5)*(2)= 25-40=-15
DELTA UJEMNA, BRAK MIEJSC ZEROWYCH.

b) y=x2+6x+8
a=1 b=6 c=8
Δ=b2-4ac=(6)2-4*(1)*(8)=36-32=4
DELTA DODATNIA,DWA MIEJSCA ZEROWE.

c) y=x2+2x+1
a=1 b=2 c=1
Δ=b2-4ac=(2)2-4*(1)*(1)=4-4=0
DELTA RÓWNA 0, JEDNO PODÓWJNE MIEJSCE ZEROWE.

Skoro ustalamy czy funkcja kwadratowa ma, czy nie ma miejsc zerowych to musimy również wiedzieć jak je obliczyć.
Jeśli Δ<0 nie liczymy miejsc zerowych, bo po prostu ich nie ma. Taka parabola może być położona w sposób przedstawiony obok.
Gdy Δ>0 funkcja kwadratowa ma dwa miejsca zerowe. Podajmy na nie wzory lub . Funkcja kwadratowa, która ma dwa miejsca zerowe może leżeć w taki sposób.
Gdy Δ=0 funkcja kwadratowa ma dwa podwójne miejsca zerowe, które wyznaczamy ze wzoru: . Funkcja kwadratowa, która ma jedno podwójne miejsce zerowe może leżeć taki sposób:


Przejdźmy teraz do zadania.

Zadanie 1.
Naszkicuj wykres funkcji kwadratowej o wzorze .

Zacznijmy od wypisania współczynników tej funkcji.
a= -1 b=-2 c=3

Ustalmy teraz w którą stronę skierowane są ramiona tej paraboli.
Sprawdzamy czy współczynnik kierunkowy „a” jest większy czy mniejszy od 0.
W naszym przypadku a=-1.
-1<0
Parabola ta ma skierowane ramiona w dół.

Obliczmy teraz współrzędne wierzchołka tej paraboli. .
Przypomnijmy wzór na „p” i podstawmy wartości współczynników z naszego zadania.




Obliczmy teraz współczynnik „q” tego wierzchołka.
Zrobimy to na dwa sposoby.

I sposób.
Współczynnik „q” wierzchołka obliczymy wstawiając w miejsce „x” wartość „p”.
Przypomnijmy wzór funkcji kwadratowej z treści naszego zadania.


Obliczmy .



4 to współrzędna „q” wierzchołka paraboli.

Pokażmy teraz II sposób.

II sposób.
W drugim sposobie wykorzystamy wzór na współrzędną „q” wierzchołka, czyli .
Musimy najpierw obliczyć deltę.




Podstawmy do wzoru.

Wyznaczyliśmy na dwa sposoby współrzędną „q” wierzchołka paraboli zatem możemy podać współrzędne wierzchołka.
W(-1;4)

Zabierzmy się teraz za sprawdzenie czy istnieją miejsca zerowe tej funkcji kwadratowej.
Obliczmy zatem deltę (możemy skorzystać z tej którą liczyliśmy wyżej, ja jednak obliczę ją jeszcze raz, żeby utrwalić Wam wzór).




DELTA WIĘKSZA OD ZERA, DWA MIEJSCA ZEROWE.

Skoro wiemy, że są dwa miejsca zerowe, to obliczmy je.

Jak widzimy w obu wzorach pojawia się .
Obliczmy zatem .
to liczba 4.

Podstawmy do wzorów na miejsca zerowe.




Jedno miejsce zerowe to punkt o współrzędnych P(1;0)

Obliczmy teraz drugie miejsce zerowe.




Drugie miejsce zerowe to punkt R(-3;0).

Dodatkową informacją, którą możemy podać znając wzór funkcji kwadratowej, to miejsce przecięcia się wykresu funkcji z osią Y, czyli osią pionową.
Jest to punkt o współrzędnych (0;c).
Zatem współczynnik „c”, który możemy podać patrząc na wzór funkcji kwadratowej, to miejsce w, którym wykres tej funkcji kwadratowej, czyli parabola przecina oś OY.
W naszym przypadku jest to punkt o współrzędnych Q(0;3)
.
Zbierzmy teraz wszystkie informacje na temat paraboli z treści naszego zadania.
Ramiona paraboli skierowane są w dół.
Wierzchołek tej paraboli to punkt W(-1;4).
Miejsca zerowe tej funkcji kwadratowej to punkty P(1;0) oraz R(-3;0).
Miejsce przecięcia się wykresu funkcji kwadratowej z pionową osią OY to punkt Q(0;3).
Znając te informacje możemy naszkicować parabolę.

Wygląda ona następująco:

Znając już schemat w jaki mamy działać rozwiążmy jeszcze jedno zadanie.

Zadanie 2.
Naszkicuj wykres funkcji kwadratowej, znając jej wzór. .

Na wstępie wypiszmy współczynniki tej funkcji kwadratowej.
a= 2 b= 4 c= 5

Ustalmy teraz w, którą stronę skierowane są ramiona tej paraboli.
a=2
2>0
Ramiona są skierowane w górę.

Podajmy teraz współrzędne wierzchołka.
Zacznijmy od obliczenia współrzędnej „p”.

Podstawmy:

Obliczmy teraz współrzędną „q”.
Zrobię to również na dwa sposoby.

I sposób.

II sposób.
Korzystamy z wzoru.

Obliczmy deltę.







Wierzchołek tej paraboli to punkt o współrzędnych W(-1;3)

Sprawdźmy teraz czy są miejsca zerowe tego trójmianu kwadratowego. Jeśli są to je obliczmy.
Liczymy ponownie deltę (można skorzystać z tej, którą liczyliśmy wyżej, ale ja policzę ją od nowa)




DELTA UJEMNA, BRAK MIEJSC ZEROWYCH.

Podajmy jeszcze punkt przecięcia się paraboli z osią pionową OY.
Wiemy, że jest to punkt Q(0,c)
Zatem w naszym przypadku jest to punkt Q(0;5)

Zbierzmy informacje na temat wykresu tej funkcji kwadratowej.
Ramiona paraboli skierowane są w górę.
Wierzchołek to punkt o współrzędnych W(-1;3)
Funkcja kwadratowa nie ma miejsc zerowych (parabola leży albo w całości nad osią poziomą OX, albo w całości pod osią poziomą OX)
Punkt przecięcia się paraboli z pionową osią OY, to punkt Q(0;5)
Naszkicujmy wykres tej funkcji kwadratowej.

Warto wiedzieć:
Inna nazwa funkcji kwadratowej to trójmian kwadratowy.
Deltę możemy inaczej nazywać wyróżnikiem trójmianu kwadratowego.
Miejsca zerowe funkcji kwadratowej to inaczej pierwiastki funkcji kwadratowej.
Trójmian kwadratowy może mieć maksymalnie dwa miejsca zerowe.
Inne punkty funkcji kwadratowej również możemy wyznaczyć. Wystarczy, że stworzymy tabelkę z kilku punktów. Każdy z nich podstawiamy do wzoru funkcji kwadratowej pod „x” i obliczamy wartość funkcji dla danego argumentu.
Funkcja kwadratowa może mieć również postać iloczynową , gdzie „a” to współczynnik kierunkowy, natomiast x1 i x2 to miejsca zerowe.
Istnieje również postać kanoniczna funkcji kwadratowej, to taka z której możemy odczytać wierzchołek paraboli tej funkcji. Ma ona postać , gdzie „a” to współczynnik kierunkowy, natomiast „p” oraz „q” to współrzędne wierzchołka

Miłej nauki!!