Planimetria

Planimetria (nazywana często geometrią płaszczyzny, „ge” – ziemia, „metreo” – mierzę) to dział geometrii, który dotyczy badania figur płaskich i ich własności, czyli płaszczyzny euklidesowej. Planimetria zajmuje się przestrzenią jednowymiarową (np. linia, punkt) i dwuwymiarową (np. trójkąt, kwadrat). Pojęciem podobnym do planimetrii jest stereometria, ale stereometria zajmuje się tylko przestrzenią trójwymiarową.

Podstawowe własności płaszczyzny:
-przez dowolne dwa punkty można poprowadzić tylko jedną prostą,
-przez dowolny punkt można poprowadzić co najmniej dwie proste,
-istnieją trzy punkty, które nie należą do jednej prostej.

Najważniejsze zagadnienia związane z planimetrią
Przestrzeń – jedno z podstawowych pojęć geometrii euklidesowej. Zbiór nadrzędny zawierający inne zbiory rozważane w danym dziale matematycznym. Przestrzeń oznaczamy grecką literą Ω, czyli omega.

Prosta – linia prosta, która jest nieograniczona, czyli nie ma początku i nie ma końca. Długości prostej nie da się określić. W geometrii euklidesowej prosta jest pojęciem pierwotnym, czyli pojęciem, który nie definiuje się.
W przypadku dwóch prostych, proste w szczególnym przypadku mogą być do siebie prostopadłe, czyli proste, które przecinają się pod kątem prostym lub równoległe, czyli proste, które mają ten sam współczynnik kierunkowy. Proste równoległe nie przecinają się.

Półprosta – linia prosta, która ma początek, ale nie ma końca, czyli z jednej strony jest ograniczona punktem, a z drugiej strony jest nieskończona.

Odcinek – linia prosta, która ma początek i ma koniec, czyli odcinek jest ograniczony dwoma punktami. Punkty będące końcem i początkiem odcinka należą do odcinka.

Do oznaczenia długości odcinka należy odcinkowi przypisać dwa punkty przykładowo A i B:

Do pokazania długości odcinka o początku w punkcie A i końcu w punkcie B używamy symbolu |AB|.
W naszym przypadku |AB| = 10. Możemy również długość odcinka oznaczać za pomocą małych liter alfabetu łacińskiego, np. a, b, c, d.

Kąt – przestrzeń między dwiema półprostymi, które mają wspólny początek. Wspólny początek półprostych nazywamy wierzchołkiem kąta, a każdą z półprostych ramieniem kąta. Do oznaczania kątów najczęściej stosuje się litery greckiego alfabetu, np. – alfa, – beta, – gamma, – delta. Miarę kąta zapisujemy w stopniach, a miarę łukową kąta w radianach. Na poniższym rysunku grecką literą oznaczono miarę kąta, a literami a i b ramiona kąta. Najprostszym przyrządem służącym do wyznaczania miary dowolnego kąta jest kątomierz.

Ze względu na miarę wyróżniamy:
-kąty zerowe (kąty o mierze 0°),
-kąty ostre (kąty o mierze należącej do przedziału (0°, 90°)),
-kąty proste (kąty o mierze 90°),
-kąty rozwarte (kąty o mierze należącej do przedziału (90°, 180°)),
-kąty półpełne (kąty o mierze 180°),
-kąty wklęsłe (kąty o mierze należącej do przedziału (180°, 360°)) ,
-kąty pełne (kąty o mierze 360°).

Ze względu na położenie kątów wyróżniamy:
-kąty przyległe (kąty, które mają wspólne ramię; oba kąty tworzą kąt półpełny, czyli kąt o mierze 180°),
-kąty naprzemianległe (kąty, które powstały przez przecięcie dwóch równoległych prostych trzecią prostą; kąty naprzemianległe leżą po przeciwnych stronach trzeciej prostej i mają takie same miary),
-kąty wierzchołkowe (kąty, których ramiona jednego kąta są przedłużeniem ramion drugiego kąta; kąty wierzchołkowe mają wspólny wierzchołek; dwa kąty wierzchołkowe leżące na przeciwko siebie mają równe miary),
-kąty odpowiadające (kąty, które powstały przez przecięcie dwóch równoległych prostych trzecią prostą; kąty odpowiadające leżą po tej samej stronie trzeciej prostej).

Trójkąt – wielokąt mający trzy boki. Trójkąt jest najmniejszą pod względem ilości boków figurą wypukłą. Trójkąt jako jedyny wielokąt nie posiada przekątnych. Suma miar kątów w dowolnym trójkącie wynosi 180°.

Podział trójkątów ze względu na boki:
-trójkąty równoboczne (wszystkie boki trójkąta mają tą samą długość),
-trójkąty równoramienne (dwa boki trójkąta mają tą samą długość),
-trójkąty różnoboczne (każdy bok ma inną długość).

Podział trójkątów ze względu na kąty:
-trójkąty ostrokątne (wszystkie kąty trójkąta są kątami ostrymi),
-trójkąty prostokątne (mają jeden kąt prosty, a pozostałe ostre),
-trójkąty rozwartokątne (jeden z kątów trójkąta jest kątem rozwartym, a pozostałe kątami ostrymi).

Wzór na obwód trójkąta:

Wzór na pole trójkąta:

Czworokąt – wielokąt mający cztery boki. Szczególnym przypadkiem czworokąta jest prostokąt, kwadrat, trapez, deltoid, równoległobok i romb. Suma miar kątów dowolnego czworokąta wynosi 360°. Boki tego czworokąta oznaczono literami a, b, c, d. Przekątne czworokątna oznaczono literami i .

Wzór na obwód (dowolnego) czworokąta:
|AB| + |BC| + |CD| + |DA|

Wzór na pole (dowolnego) czworokąta:

Kwadrat – czworokąt, który ma wszystkie kąty proste i wszystkie boki tej samej długości. Przekątne kwadratu przecinają się w połowie oraz są tej samej długości. Znając długość boku kwadratu można obliczyć jego przekątną. Przekątną kwadratu obliczamy za pomocą wzoru: . Kwadrat jest również nazywany czworokątem foremnym. Każdy kwadrat jest również prostokątem. Na poniższym rysunku wszystkie boki kwadratu oznaczono literą a.

Wzór na obwód kwadratu:

Wzór na pole kwadratu:

Prostokąt – czworokąt, którego wszystkie kąty są proste. Prostokąt posiada dwie pary boków tej samej długości i dwie pary boków są do siebie równoległe. Szczególnym przypadkiem prostokąta jest kwadrat. Przekątne każdego prostokąta są tej samej długości i przecinają się w połowie. Długość przekątnej prostokąta obliczamy ze wzoru:
. Na poniższym rysunku boki o tej samej mierze oznaczono literami a i b.

Wzór na obwód prostokąta:

Wzór na pole prostokąta:

Trapez – czworokąt, który posiada co najmniej jedną parę boków równoległych. Na poniższej ilustracji trapezu literami a i b oznaczono podstawy trapezu, a literami c i d ramiona trapezu, h jest jego wysokością prostopadłą do podstawy. Szczególnymi przypadkami trapezu jest trapez równoramienny oraz trapez prostokątny.

Wzór na obwód trapezu:

Wzór na pole trapezu:

Szczególne przypadki trapezu:
-trapez równoramienny (trapez, którego ramiona są tej samej długości; przekątne trapezu są tej samej długości; kąty przy podstawie są tej samej długości),
-trapez prostokątny (trapez, którego co najmniej jedno ramię jest prostopadłe do podstaw; szczególnym przypadkiem trapezu prostokątnego jest prostokąt i kwadrat).

Deltoid – czworokąt, którego przekątne są do siebie prostopadłe, a jedna z nich jest symetralna drugiej. Według większości źródeł romb jest deltoidem, ale, np. według polskiego matematyka Jana Zydlera, deltoid nie może mieć wszystkich boków tej samej długości. Na poniższym rysunku boki o tej samej długości oznaczono literami a i b. Przekątna jest prostopadła do przekątnej .

Wzór na obwód deltoidu:

Wzór na pole deltoidu:

Równoległobok – czworokąt, który ma dwie pary boków równoległych. Boki, które są do siebie równoległe w równoległoboku mają tą samą długość. Równoległobok jest również trapezem, ponieważ zgodnie z definicją trapezu, trapezem jest ten czworokąt, który posiada co najmniej jedną parę boków równoległych. Szczególnym przypadkiem równoległoboku jest prostokąt, ponieważ posiada wszystkie kąty proste. Na poniższym rysunku boki o tej samej długości oznaczono literami a i b. Wysokość równoległoboku jest prostopadła do jego podstawy.

Wzór na obwód równoległoboku:

Wzór na pole równoległoboku:

Romb – czworokąt, którego wszystkie boki są tej samej długości. Każdy romb ma dwie pary boków równoległych. Każdy romb jest również równoległobokiem, ponieważ spełnia jego definicję. Każdy romb jest także deltoidem, gdyż jego przekątne przecinają się w połowie. Kwadrat jest szczególnym przypadkiem rombu, ponieważ wszystkie kąty kwadratu są kątami prostymi. Boki o tej samej długości na poniższym rysunku oznaczono literą a. Przekątne rombu oznaczono literami e i f.

Wzór na obwód rombu:

Wzór na pole rombu:

Okrąg – zbiór punktów na płaszczyźnie równoodległych od środka okręgu. Potocznie okrąg jest nazywany brzegiem koła albo obrączką. Literą S oznaczono środek okręgu. Należy pamiętać, że środek okręgu nie należy do okręgu! Przyrządem służącym do szkicowania okręgów jest cyrkiel.

Pojęcia związane z okręgiem:
-środek (punkt znajdujący się w miejscu przecięcia się dwóch średnic okręgu),
-promień (odcinek o początku w środku okręgu i końcu na okręgu),
-średnica (cięciwa, która przechodzi przez środek okręgu),
-cięciwa (odcinek, który łączy dwa punkty leżące na okręgu).

Styczna do okręgu – prosta, która ma jeden punkt wspólny z okręgiem. Styczna zawsze jest prostopadła do promienia tego okręgu. Miejscem, w którym styczna ma punkt wspólny z okręgiem nazywamy punktem styczności.

Sieczna do okręgu – prosta, która ma dwa punkty wspólne z okręgiem. Na poniższym rysunku punkty wspólne prostej z okręgiem oznaczono literami A i B.

Koło – zbiór punktów na płaszczyźnie, których odległość od środka jest mniejsza lub równa promieniowi tego koła.
Koło jest ograniczone okręgiem. W kole tak jak w okręgu wyróżniamy promień, średnicę i cięciwę. Opisy tych pojęć znajdują się powyżej.

Ciekawostka
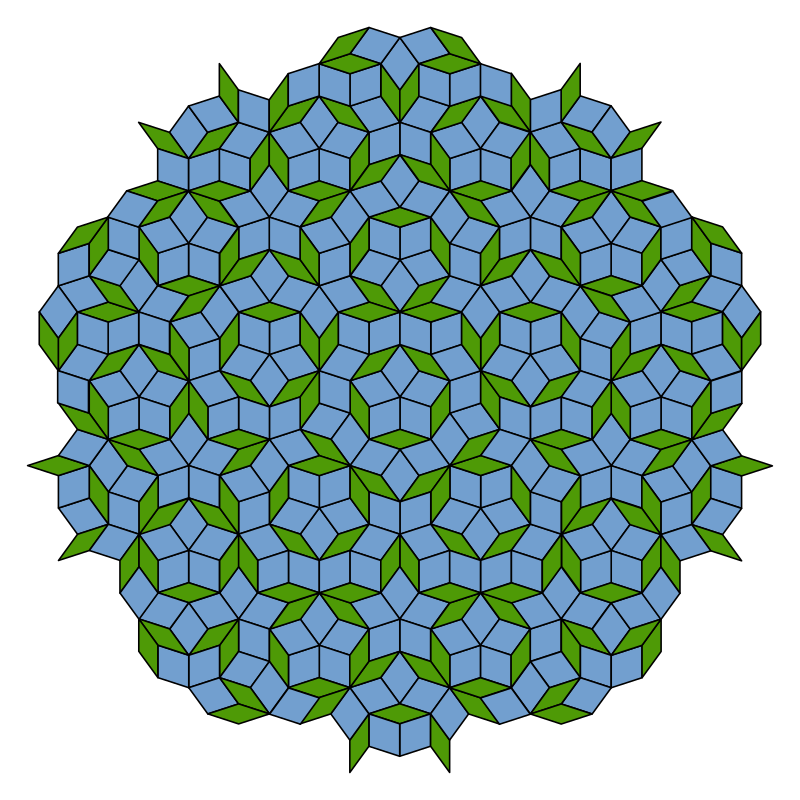
Roger Penrose odkrył, że z dwóch rodzajów figur geometrycznych – rombów (należących do działu „Planimetria”) można wykonać parkietaż. Parkietaż Penrose’ a polega na pokryciu płaszczyzny przez dwa rodzaje figur. Wzór nie może powtarzać się okresowo. W parkietażu dwa stykające się ze sobą romby nie mogą przedstawiać równoległoboku.

Na powyższej ilustracji jest przedstawiony jeden z najpopularniejszych rodzajów parkietaży Penrose’a.

Na powyższej ilustracji znajduje się parkietaż, który nie spełnia tzw. „reguły równoległoboku”. Przykładowy równoległobok widoczny na parkietażu został zaznaczony czarnymi liniami.