Opracowanie:
Pole powierzchni stożka
Pole powierzchni stożka
Pole powierzchni stożka
Własności stożka:
trójkąt jest przekrojem osiowym
powstaje poprzez obrót trójkąta
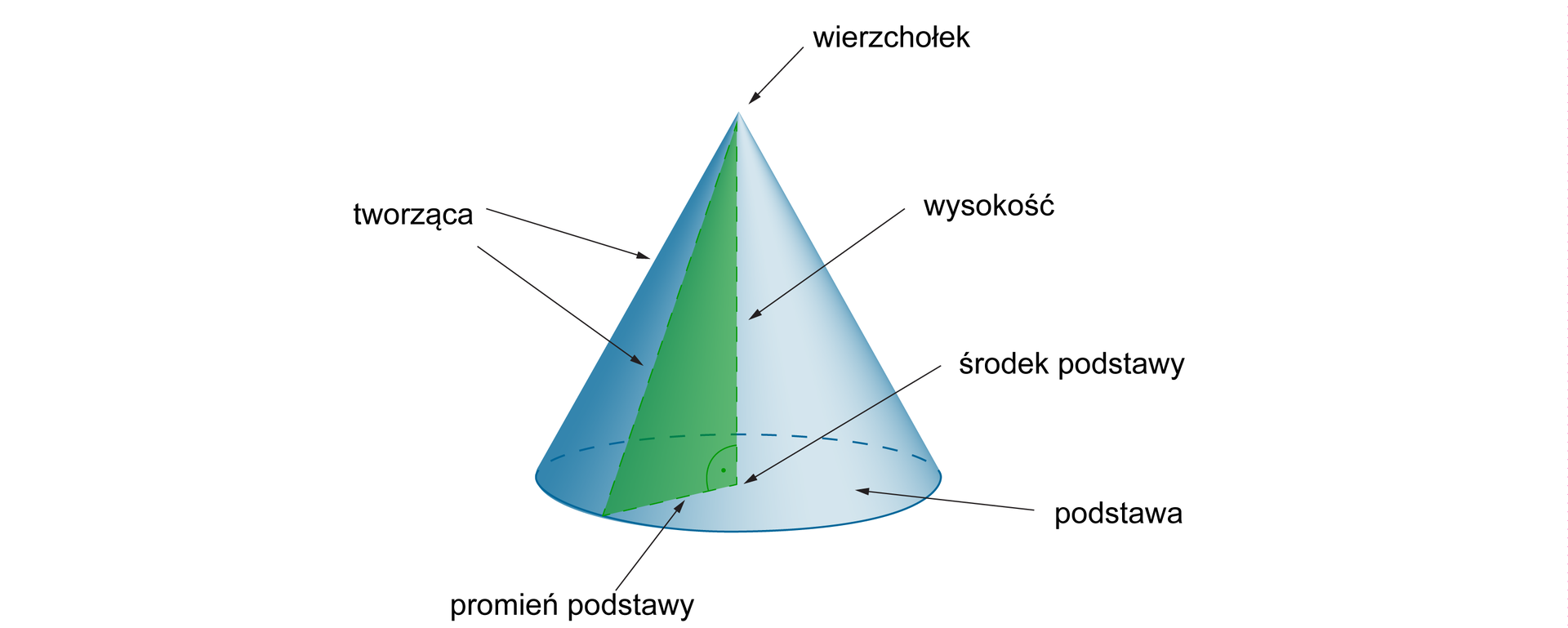
literą l oznaczamy tworzącą stożka
literą V oznaczamy objętość stożka
Na poniższej ilustracji znajduje się przykładowy stożek oraz nazwy jego poszczególnych elementów:
Rodzaje stożków:
2. 3.
stożek prosty
stożek ścięty
stożek pochyły
Pole powierzchni całkowitej stożka – suma pola podstawy i powierzchni bocznej stożka.
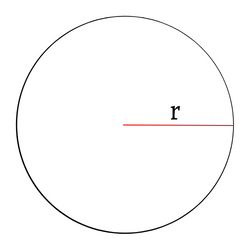
Pole podstawy stożka liczy się ze wzoru:
Pp = π*r2
By wyznaczyć pole powierzchni bocznej stożka, należy najpierw obliczyć kąt rozwarcia α:
D = (2*π*l) : 360 *α
α = (360r) : l
Pole wycinka pola wynosi:
Pw = (π*l2*α) : 360
Pw = π*r*l
Dzięki temu możemy obliczyć całkowitą powierzchnię stożka:
Pc = Pp + Pw = π*r2 + π*r*l = π*r*(r+l)
Pc = π*r*(r+l)
π=3,1415926535897932384626433832795
Przykład zadania z obliczaniem powierzchni całkowitej stożka: