Pole równoległoboku wzór

Pole równoległoboku wzór
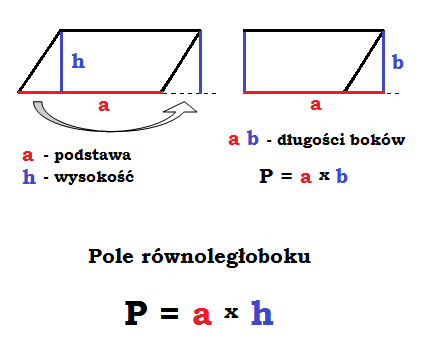
Żeby można było oblicz pole równoległoboku (czyli jego powierzchnie) wystarczy zapamiętać wzór. W przypadku równoległoboku jest to podstawa pomnożona razy wysokość, czyli:
P =
Gdzie a to podstawa, a h to wysokość.

Taki prosty wzór wziął się stąd, że gdybyśmy zrobili z kawałka równoległoboku trójkąt i dali go w inne miejsce to otrzymalibyśmy prostokąt, a wzór na prostokąt to a razy b. Tutaj wzór jest taki sam tylko jest nie razy b, lecz razy h ponieważ w równoległoboku jest to wysokość, a nie bok. Zobacz na przedstawienie tego wizualnie na poniższym rysunku:

Jednostka, w której najczęściej podaje się pole równoległoboku to centymetry kwadratowe. Czasami przy liczeniu nie ma żadnej jednostki, wówczas w wyniku również nie trzeba żadnej dawać. Wystarczy zostawić liczbę bez niej.

Przykład 1
Wysokość równoległoboku to 6 centymetrów, a jego podstawa to 11 centymetrów. Na tej podstawie oblicz jego pole. Wynik zapisz w centymetrach.

Najpierw zapisujemy dane.

dane:
Wysokość – 6 cm
Podstawa – 11 cm

Teraz możemy napisać to czego szukamy.

Szukana:
pole – ?

Teraz napiszmy pole na równoległobok i podstawmy dane pod wzór:

Dzięki wzorowi doszliśmy do wyniku, czyli pola tego równoległoboku.

Odpowiedź: Pole tego równoległoboku ma 66 centymetrów kwadratowych.

Zadanie 1
Oblicz pole równoległoboku, którego wysokość to 5 centymetrów, a podstawa 6.

=

Zadanie 2
Oblicz pole równoległoboku, jeżeli jego podstawa jest dwa razy większa niż wysokość, a wysokość jest dwa razy większa niż trzy centymetry.

Do rozwiązania tego zadania na początku musi zostać obliczona wysokość, ponieważ nie można policzyć podstawy gdyż jest tylko powiedziane jak się ona ma do wysokości. Wysokość jest dwa razy większa niż dwa centymetry, musimy więc znaleźć liczbę, która jest dwa razy większa niż trzy.
Wysokość – liczba dwa razy większa niż trzy – 2 3 cm = 6 cm

W związku z tym, że mamy już wysokość to możemy obliczyć podstawę. Jest ona dwa razy większa niż wysokość. Musimy więc pomnożyć ją razy dwa.

podstawa – 2 6 cm = 12 cm

Teraz możemy podstawić liczby te pod wzór:

cm

Zadanie 3
Pewien równoległobok ma wysokość 9 centymetrów, a podstawę 14 centymetrów. Oblicz jego pole.

Można na początku wypisać dane, które posiadamy, a do tego dopisać szukaną, czyli pole:
dane:
podstawa – 14 centymetrów
wysokość – 9 centymetrów
szukana:
P = ?

Na takich liczbach nie jest łatwo wyliczyć pola. Można zrobić to z kalkulatorem, jednak jest też jeden sposób dzięki, któremu możemy to zrobić w pamięci. Wystarczy najpierw podzielić dziesięć razy dziewięć, a potem jeszcze cztery (które zostały) razy dziewięć:
14 9 = 10 9 + 4 9 = 90 + 36 = 126

Odpowiedź: Pole tego równoległoboku wynosi 126 cm.

Zadanie 4
Oblicz pole równoległoboku. Jego podstawa ma 80 mm, a wysokość 5 cm. Oblicz jego pole, wynik zapisz w centymetrach.

Najpierw należy zamienić wszystkie jednostki na tą samą, inaczej się tego zrobić nie da. W tym przypadku lepiej zamienić na centymetry. Normalnie nie miało by to różnicy, ale teraz i tak musimy wynik zapisać w centymetrach.

podstawa – 80 mm – 8 cm
wysokość – 5 cm

Teraz można obliczyć dzięki temu pole:

Odpowiedź: Pole tego równoległoboku wynosi .

równoległoboki – romby, prostokąty, kwadraty
Romby, kwadraty i prostokąty to również rodzaje równoległoboków. Jeżeli równoległobok ma wszystkie kąty proste (tak jak w zadaniu piątym, w podpunkcie a) to jest prostokątem, natomiast jeśli ma wszystkie boki równe to jest on rombem. W sytuacji, gdy równoległobok nie tylko ma wszystkie boki równe, ale i jest równocześnie prostokątem to jest to kwadrat.

Zadanie 5
Oblicz pola poniższych równoległoboków. Długość każdej kratki wynosi jeden.

a)
wysokość – 3
podstawa – 5
P =

b)
wysokość – 3
podstawa – 5
= 15

c)
wysokość – 3
podstawa – 5

d)
wysokość – 3
podstawa – 5

Mimo iż wszystkie z tych równoległoboków wyglądają inaczej, to i tak każdy ma pole 15. Pierwszy z nich to równoległobok, ale też równocześnie prostokąt.