Przekątne rombu

Romb jest płaską figurą geometryczną. Ponadto, jest on szczególnym przypadkiem równoległoboku, ponieważ jego boki są tej samej długości. Kwadrat zaś, jest szczególnym przypadkiem rombu, gdyż każdy z czterech kątów wewnętrznych jest tej samej miary i wynosi dokładnie 90°. Z tego wynika, że jego obwód rombu wynosi , gdzie a jest bokiem naszego rombu.

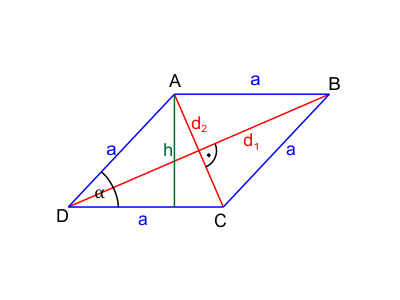
Jak widzisz, romb posiada dwie przekątne. Przekątne te przecinają się pod kątem prostym. Punkt przecięcia dzieli każdą z przekątnych na dwa odcinki o tej samej długości. Tym samym, prowadząc przekątne, tworzymy cztery trójkąty prostokątne o tym samym polu powierzchni. Skoro więc są to trójkąty prostokątne, rozwiązując zadania często będziemy mogli je rozwiązać stosując twierdzenie Pitagorasa.

Zauważ, że jak w każdym równoległoboku możemy narysować wysokość. W rombie też możemy.

Gdybyśmy wpisali w ten romb okrąg, to jego środkiem byłby punkt przecięcia się przekątnych. Co ważne, promień tego wpisanego okręgu miałby długość połowę mniejszą niż wysokość.

zadanie 1
Został narysowany romb, którego przekątne wynoszą odpowiednio 6 oraz 16cm. Dodaj, ile wynosi bok tego rombu.

Rozwiązanie takiego zadania zaczynamy od narysowania rombu. Następnie prowadzimy przekątne. Podpisujemy długości boków otrzymanych trójkątów. Spójrz teraz na dowolny z trójkątów. W każdym z nich przeciwprostokątna, a więc bok naszego rombu jest niewiadomą.

Założenia: a > 0

Zastosujmy więc po prostu twierdzenie Pitagorasa:

Podstawiamy dane do twierdzenia

Podnosimy do kwadratu

Sumujemy prawą stronę równania

Pierwiastkujemy otrzymując wynik

Odpowiedź: Bok naszego rombu to .

Oczywiście, mamy w matematyce jeszcze wzory, które pozwalają nam na obliczanie długości dłuższej oraz krótszej przekątnej.

W obu przypadkach długość boku jest oznaczona literką a.

zadanie 2
Został narysowany romb, w którym krótsza przekątna oraz bok są tej samej długości. Wyraź, ile będzie wynosić dłuższa przekątna, wiedząc, że krótsza przekątna i bok to a.

Oczywiście zaczynamy od rysunku.

Zauważ, że krótsza przekątna podzieliła nam romb na dwa takie same trójkąty równoboczne.

Jak wiesz, wysokość takiego trójkąta możemy policzyć z wysokości w trójkącie równobocznym. Ten wzór oczywiście znajduje się w tablicach maturalnych.

Oznaczmy sobie dłuższą przekątną jako

Odpowiedź: Dłuższa przekątna w tym rombie to

zadanie 3
Oblicz pole rombu, którego przekątne to odpowiednio 4cm oraz 6cm.

Rozwiązanie zadania zaczynamy od wypisania danych.

Dane:

Następnie podstawiamy do wzoru.

Odpowiedź: Pole tego rombu wynosi

zadanie 4
Pewien romb ma pole . Jego krótsza przekątna nie jest nam znana. Oblicz jej długość wiedząc, że dłuższa przekątna wynosi 140cm.

Rozwiązanie takiego zadania zaczynamy od wypisania danych. Zauważamy, że mamy tutaj różne jednostki. Dlatego też zaczynamy od zapisania tych danych we wspólnych jednostkach. Polecam zamienienie je na decymetry.

Dane:

I sposób rozwiązania zadania

Podstawiamy dane do gotowego wzoru na krótszą przekątną (e)

Odpowiedź: Krótsza przekątna jest długości 8dm.

II sposób rozwiązania zadania

Zapisujemy wzór na pole powierzchni rombu

Podstawiamy dane do wzoru oraz mnożymy obustronnie przez dwa

Zapisujemy obliczenia

Obustronnie dzielimy przez współczynnik

Zapisujemy wynik

Odpowiedź: Krótsza przekątna jest długości 8dm.