Opracowanie:
Przestrzeń
Przestrzeń
Przestrzeń ogólnie oznacza wszystko, co nas otacza, bądź to, co otacza jakieś ograniczone miejsce. Głównie kojarzy się z fizyką. W matematyce natomiast przestrzeń to zbiór, który zawiera inne zbiory. Zwana też jest strukturą matematyczną.
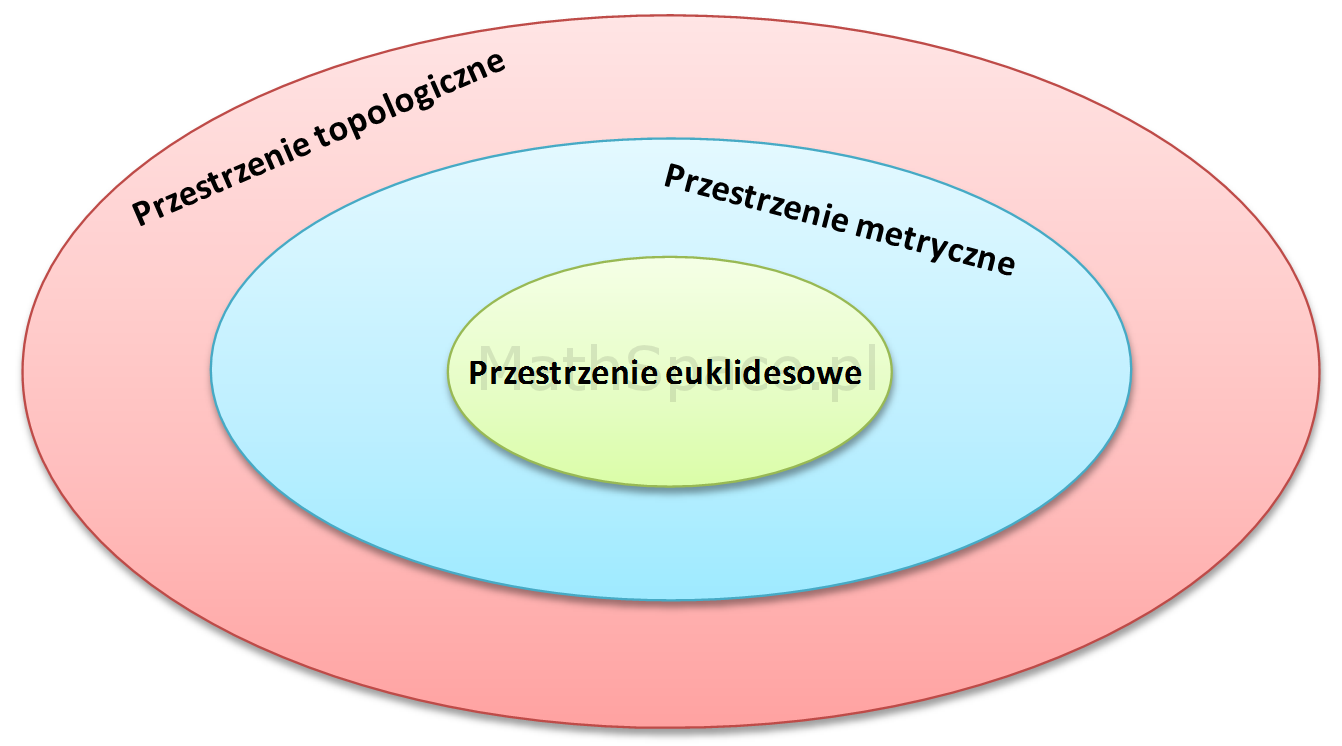
Przestrzenie w matematyce mogą tworzyć hierarchię od najbardziej szczególnych do najbardziej ogólnych.
Wyróżniamy wiele rodzajów przestrzeni w matematyce.
Przestrzenie mogą być ilorazowe, czyli takie, gdzie typ elementów zbioru ma zdefiniowane relacje i działania.
Kolejnym rodzajem przestrzeni jest przestrzeń liniowa. Jest to zbiór elementów, w którym określono dwa działania:
-dodawanie wektorów
-skalowanie, czyli mnożenie wektorów przez skalar, czyli przez liczby z danego ciała
Przykładowo można sprawdzić czy W jest podprzestrzenią liniową przestrzeni V nad ciałem K.
Uznajmy, że „v” i „w” należą do W, a „y” należy do K.
v, w W
y K
Jeżeli:
v + w W
y * v W
W jest podprzestrzenią Z wtedy, i tylko wtedy gdy powyższe warunki są spełnione.
Wyróżniamy również przestrzeń Banacha, czyli przestrzeń unormowana X, w której metryka „d” wyznaczona jest przez normę. Określa się to wzorem:
d (x, y) = ll x – y ll
x, y X
Przestrzeń Banacha pochodzi od nazwiska Stefana Banacha, który zmarł ponad 70 lat temu, a który skromnie owe przestrzenie nazwał przestrzeniami B. Przestrzeń Banacha to przestrzeń liniowa, której elementami są wektory. Można mierzyć w niej odległość między obiektami, czyli przestrzeń ta jest unormowana. Sposób pomiaru odległości w każdym miejscu przestrzeni musi być taki sam. W przestrzeni Banacha nie może być żadnych przerw ani szczelin, czyli przestrzeń ta musi być zupełna.
Kolejną przestrzenią jest przestrzeń Hilberta, czyli przestrzeń liniowa nad ciałem liczb rzeczywistych, która posiada iloczyn skalarny. Jest to przestrzeń metryczna oraz posiada właściwości przestrzeni zupełnej.
Przykładem przestrzeni Hilberta jest przestrzeń euklidesowa, która dobrze określa przestrzeń fizyczną. Za jej pomocą opisuje się odległości makroskopowe.
Przykład wygląda następująco:
Mamy też przestrzeń topologiczną, gdzie zbiór X wraz z rodziną podzbiorów r, które spełniają odpowiednie własności. Rodzina r to topologia na zbiorze X, a jej elementy to zbiory otwarte w X.
Np. funkcja f: R R jest ciągła wtedy, i tylko wtedy, gdy f-1 (U) dowolnego zbioru U R jest otwarty.
Kolejną przestrzenią jest przestrzeń trójwymiarowa. Jest to przestrzeń euklidesowa o trzech wymiarach. Każdemu punktowi tej przestrzeni odpowiada uporządkowana trójka liczb rzeczywistych.
Przykładowo wygląda to tak:
Kolejną przestrzenią jest przestrzeń spójna. Jest to przestrzeń topologiczna, której nie można rozłożyć na sumę dwóch rozłącznych, niepustych podzbiorów otwartych.
Mamy również przestrzeń zupełną, czyli przestrzeń metryczną o takiej własności, że każdy zbieżny ciąg utworzony z punktów tej przestrzeni ma granicę w punkcie należącym do tej przestrzeni.
Przestrzeń mierzalna, czyli przestrzeń z wyróżnioną rodziną jej zbiorów nazywaną σ-ciałem. Przestrzenie te bada się w teorii mnogości, teorii miary i rachunku prawdopodobieństwa.
Jeżeli X jest przestrzenią, a F rodziną zbiorów przestrzeni X. Rodzinę F przestrzeni X nazwiemy σ-ciałem jeśli:
-zbiór pusty należy do F
Ø F
-dopełnienie zbioru, czyli zbiór wszystkich elementów, które do danego zbioru nie należą, należącego do F należy do F
A F X; A F
-suma przeliczalnie wielu zbiorów, czyli zbiorów skończonych należących do F należy do F
Kolejną przestrzenią jest przestrzeń probabilistyczna. Umożliwia ona opis procesu losowego poprzez określenie przestrzeni zdarzeń elementarnych oraz określenie na jej podzbiorach funkcji prawdopodobieństwa. Przestrzeń ta to trójka Ω, F i P
1) Ω – to zbiór niepusty
2) F – to rodzina podzbiorów zbioru Ω.
W tym przypadku:
-∅ ∈ F
-jeżeli A ∈ F, to Ac = Ω A ∈ F
-jeżeli A1, A2, . . . ∈ F, to ∞S n=1 An ∈ F
3) P to funkcja
P : F −→ [0, 1]
W tym przypadku:
-P(Ω) = 1
-dla A1, A2, . . . ∈ F
Występuje również półprzestrzeń, gdzie każdą z dwóch części przestrzeni dzieli płaszczyzna, wraz z ta płaszczyzną lub bez niej.