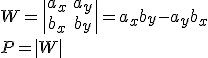Równoległobok pole

Zapewne znacie ze szkoły prostą definicję równoległoboku „czworokąt, który ma dwie pary boków równoległych”, a pierwsze co przychodzi Wam na myśl to figura z poniższego obrazka.

W moim wypracowaniu postaram się zdefiniować równoległobok na wszystkie możliwe sposoby.

Zacznijmy od tego, że równoległobok definiujemy jako figurę geometryczną, co oznacza, że jest to zbiór punktów w przestrzeni. Właściwie to zbiór punktów należących do jednej płaszczyzny, co z kolei definiuje równoległobok jako figurę płaską.

Jako figura płaska równoległobok posiada pewne własności, takie jak na przykład:
> wypukłość – oznacza to, że każdy odcinek, którego końce należą do figury, zawiera się w tej figurze. Tak jak na poniższym rysunku

figura wypukła figura niewypukła (wklęsła)

Z tą własnością wiąże się również spójność.

> ograniczoność – oznacza to, że zawiera się w pewnym kole.

Jeżeli nie można znaleźć koła, w którym zawiera się dana figura, to powiemy, że jest ona nieograniczona.
Przykładem figury nieograniczonej będzie np. prosta.

Przekątne równoległoboku przecinają się w połowie.

Ciekawostka 1.
Przekątna równoległoboku dzieli go na dwa trójkąty przystające.

Ciekawostka 2.
Przekątne równoległoboku dzielą go na cztery trójkąty o równej powierzchni.

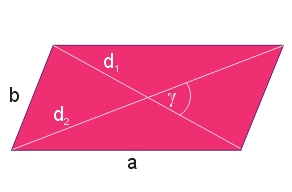
Długości przekątnych równoległoboku możemy policzyć z poniższego wzoru, jeżeli znamy boki oraz kat alpha między nimi.
krótsza przekątna =
dłuższa przekątna =

Kąty przeciwległe równoległoboku są sobie równe.

Przeciwległe boki równoległoboku są równoległe i tej samej długości, a co za tym idzie kwadrat, prostokąt oraz romb to również równoległoboki.

Co ciekawe równoległobok jest szczególnym przypadkiem trapezu.

Pole równoległoboku można zatem obliczyć na kilka sposobów, w zależności od danych podanych w zadaniu.

Wzór 1.

lub

Wzór 2.

d1 , d2 – długości przekątnych
– kąt między przekątnymi

Wzór 3.

P = a b

ale także, ze wzoru na pola prostokąta ( P = a b ), rombu ( P = (e f) /2 ) czy trapezu ( P = (a + b) h /2 )

Obwód to oczywiście suma wszystkich boków. Obliczamy go ze wzoru: Obw = 2 a + 2 b

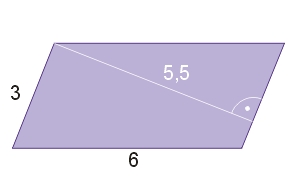
Przykład 1. Oblicz pole równoległoboku.
(Skorzystamy ze wzoru nr 1)

Dane: Szukane:
a = 6 P = ?
b = 3
h = 5,5

Rozwiązanie:
P = b h
P = 3 5,5 = 16,5

Przykład 2. Oblicz pole równoległoboku o bokach 3 i 4, którego kąt ostry wynosi 30o.
(Skorzystamy ze wzoru nr 3)
Dane: Rozwiązanie:
a = 4 P = a b
b = 3 P = 3 4 = 3 4 = 6
= 30o

Jak już wiemy równoległobok jest zbiorem punktów na płaszczyźnie, zatem jeśli w zadaniu mamy podane współrzędne wierzchołków,
przy obliczaniu pola możemy skorzystać z poniższego wzoru.

Na poniższym przykładzie wytłumaczę dokładnie o co chodzi.

Przykład 3.
Mamy podane współrzędne wierzchołków A=(1 ,1), B=(5 ,1), C=(7 ,3), D=(3, 3)

A=(1 ,1 ), D=(3 ,3 )
a = [3 – 1,3 – 1] = [2, 2]

A=(1 ,1 ), B=(5 ,1 )
b = [5 – 1,1 – 1] = [4, 0]