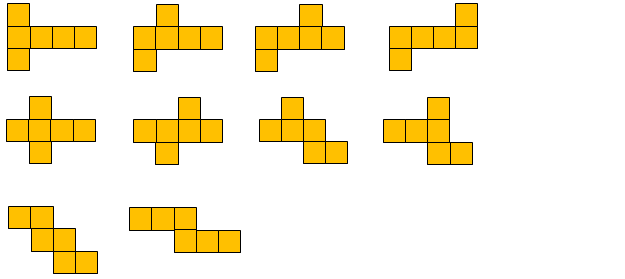Siatka sześcianu

Generalnie rzecz ujmując siatka w pojęciu matematycznym jest pewnego rodzaju modelem do składania. Możemy spotkać się z siatkami ostrosłupów, prostopadłościanów, sześcianów itd.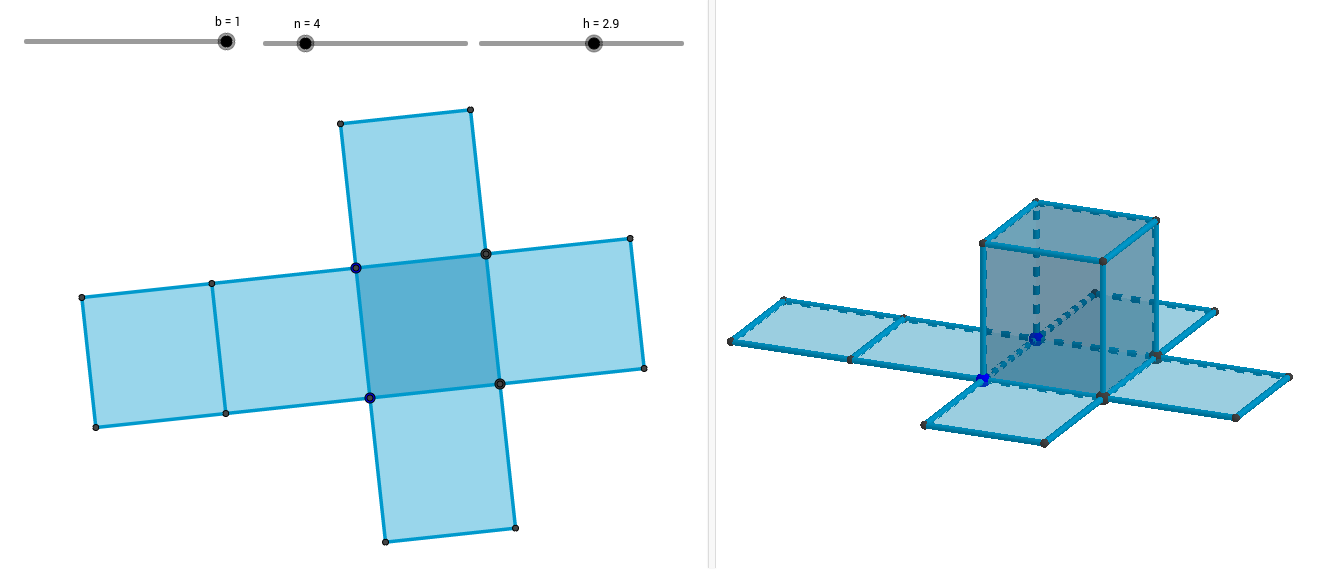

My zajmiemy się dziś sześcianami.

Jak wiesz, sześcian charakteryzuje się tym, że każda jego krawędź jest tej samej długości. Długość, szerokość i wysokość zazwyczaj oznaczamy literką a.

Jeśli byśmy wyobrazili sobie, że powyższa figura jest pudełkiem, to moglibyśmy te pudełko rozłożyć. Otrzymalibyśmy wtedy płaską figurę. Ta powstała płaska figura jest niczym innym jak siatką sześcianu.

W zależności od tego jak byśmy rozłożyli te pudełko, taką siatkę otrzymamy. Powyżej masz pokazane wszystkie siatki sześcianów jakie istnieją. Jak więc widzisz, każda siatka składa się z sześciu części. Każda z części siatki to jedna z sześciu ścian sześcianu. Znając więc długość jednej z krawędzi możemy obliczyć bardzo wiele rzeczy.
Przede wszystkim znając jedną krawędź sześcianu możemy obliczyć objętość takiej „poskładanej” bryły. Jak wiesz, obliczenie objętości bryły polega na pomnożeniu długości, wysokości oraz szerokości. W przypadku sześcianu każda krawędź jest tej samej długości, więc wzór na objętość sześcianu wyraża się jako: . Należy zawsze pamiętać o jednostkach, które w przypadku objętości są podniesione do trzeciej potęgi. Jeśli więc nasz bok wyrażony jest w centymetrach, to objętość będzie wyrażona w centymetrach sześciennych.
Zobrazowanie siatki sześcianu pozwala nam również na obliczenie pola powierzchni bocznej. Wiemy, że sześcian ma 4 ściany boczne. W takim razie, aby obliczyć pole powierzchni bocznej wystarczy pomnożyć pole powierzchni jednej ściany o krawędzi a razy cztery, a więc:
Narysowanie siatki sześcianu pozwala także na obliczenie pola powierzchni podstawy/podstaw. Wiemy, że sześcian ma 2 podstawy. Na jednej podstawie sześcian „stoi” a druga jest równoległa do pierwszej podstawy. W takim razie, aby obliczyć pole jednej podstawy wystarczy oblicz pole powierzchni jednej ściany o krawędzi a, a więc: .
Zobaczenie siatki sześcianu ponadto umożliwia nam obliczenie pola powierzchni całkowitej naszej bryły. Jak wiesz, sześcian ma dwie podstawy oraz 4 ściany. Co do powierzchni oraz wymiarów, pole jednej podstawy jest równe polu jednej ze ścian. Tak samo jest z wymiarami. Dlatego też możemy powiedzieć, że pole powierzchni sześcianu jest równe sześciu pól powierzchni jednej ściany. Pole powierzchni całkowitej sześcianu to:

Wszystkie te własności bez problemu możemy odczytywać z siatki sześcianu. Spróbujmy rozwiązać kilka zadań związanych z siatkami sześcianów.

zadanie pierwsze
Określ, które z rysunków poniżej przedstawiają siatkę sześcianu.

1.

2.

3.

4.

5.

6.

Rozwiązanie:
Spójrz na rysunek. Czy jesteś w stanie z tej siatki poskładać zamknięta pudełko? Niestety nie. Gdybyśmy ścianę z czerwonym znakiem x ujęli jako podstawę, to ściana zaznaczona na czarno w kółeczko nie miałaby swojego miejsca. Nie jest to siatka sześcianu.
Czy z tej siatki możemy stworzyć sześcian? Nie. Gdybyśmy ścianę z czerwonym znakiem x ujęli jako podstawę, to ściana zaznaczona na czarno w kółeczko nie miałaby swojego miejsca. Nie jest to siatka sześcianu.
Czy to jest siatka sześcianu? Spójrz na rysunek. Wyobraźmy sobie, że czerwony x jest narysowany na dolnej podstawie. Równoległa do niej podstawa została zaznaczona na fioletowo. W takim razie możemy z tej siatki stworzyć zamknięte „pudełko” jakim jest sześcian. Tak, to jest siatka sześcianu.
Aby była to siatka sześcianu, każda z ścian musi być połączona z inną ścianą przynajmniej jedną krawędzią. Ścianka zaznaczona czarnym kółeczkiem nie jest połączona z żadną inną ścianą przez krawędź. To nie jest siatka sześcianu.
Czy jest to siatka sześcianu? Gdybyśmy ścianę z czerwonym znakiem x wzięli za podstawę, to ściana zaznaczona na czarno w kółeczko nie miałaby swojego miejsca. Nie jest to siatka sześcianu.
Wyobraźmy sobie, że czerwony x jest narysowany na dolnej podstawie. Równoległa do niej podstawa została zaznaczona na fioletowo. Czy w takim razie możemy stworzyć z tej siatki sześcian? Tak, gdyż z ścian tworzących siatkę sześcianu możemy stworzyć zamknięte pudełko. To jest siatka sześcianu.

Zadanie 2
Oblicz objętość oraz pole powierzchni całkowitej sześcianu, którego siatka jest przedstawiona poniżej.

Rozwiązanie zadania zaczynamy od odczytania danych.

a = 3

Czas podstawić dane do wzorów:

Odpowiedź: Objętość sześcianu, którego siatka została przedstawiona powyżej wynosi 27 (jednostek sześciennych), a pole powierzchni całkowitej wynosi 54 (jednostek kwadratowych).