Sin 45

Sin 45 – to wartość funkcji trygonometrycznej dla kąta o mierze 45 stopni, który wynosi . Funkcja trygonometryczna dotyczy trójkąta prostokątnego, w którym boki tworzą dwie przyprostokątne oraz przeciwprostokątna. Przyprostokątne mają wspólny punkt i leżą przy kącie prostym, czyli kącie o mierze 90°, a przeciwprostokątna leży naprzeciw kąta prostego.

Wartości funkcji trygonometrycznych dotyczą kątów ostrych w trójkącie prostokątnym. Na poniższym rysunku jeden z kątów oznaczymy literką . Oznacza to, że nasze rozważania dotyczące sin 45° będą dotyczyć naszego oznaczonego kąta. Dodatkowo przyprostokątne oznaczono literami i , a przeciwprostokątną literą .

Definicje funkcji trygonometrycznych względem kąta w zakresie od 0° do 90°.
1 . Sin – czytaj „sinus” to stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej.

2 .cos – czytaj „kosinus” to stosunek przyprostokątnej leżącej przy kącie do przeciwprostokątnej.

3 . tg – czytaj „tangens” to stosunek przyprostokątnej leżącej naprzeciw kąta do przyprostokątnej leżącej przy kącie

4 . ctg – czytaj „kotangens” to stosunek przyprostokątnej leżącej przy kącie do przyprostokątnej leżącej naprzeciw kąta .

Wartości funkcji trygonometrycznych dla kątów najczęściej używanych w zadaniach matematycznych:

Zadanie:
Korzystając z funkcji trygonometrycznych oblicz, jaką długość ma podstawa , czyli przeciwprostokątna trójkąta prostokątnego, równoramiennego, którego przyprostokątna ma długość
Rozwiązanie:
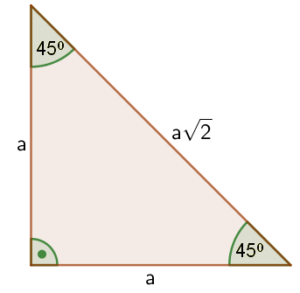
W pierwszej kolejności należy sporządzić rysunek poglądowy:

Ponieważ jest to trójkąt prostokątny równoramienny, a suma kątów wewnętrznych trójkąta wynosi 180 stopni, to odejmując 90 stopni -kąt prosty, to pozostałe kąty ostry mają miarę po 45 stopni każdy. W naszym zadaniu szukamy niewiadomej .
Skorzystamy z definicji sin 45°. Jest to stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej, czyli:


/:

Odpowiedź: długość podstawy trójkąta wynosi 2.

Własności funkcji
1 . dziedziną funkcji jest zbiór liczb rzeczywistych
2 . przyjmuje wartości <-1; 1>
3 . funkcja nie jest parzysta
4 . funkcja nie jest różnowartościowa
5 . funkcja jest okresowa. Oznacza to, że jej okres podstawowy wynosi π
6 . miejsca zerowe funkcji: π
7 . monotoniczność funkcji: jest monotoniczna przedziałami:
rosnąca: < >
malejąca: < >
8 . wykresem funkcji sinus jest sinusoida. Dla sinusoida ma postać:

Ciekawostka:
Sinusoida tworzy charakterystyczną „falę”, którą wydaje m.in. gitarowa struna, woda do której wrzucono kamyk, a także prąd w gniazdku elektrycznym. Oczywiście, aby to zobaczyć wymagany jest specjalny sprzęt. Sinus często wykorzystywany jest do tworzenia ciekawych efektów wizualnych.

Zadanie:
W trójkącie prostokątnym, w którym jeden bok ma długość 7 cm, jeden kąt ostry ma miarę 45°, dwa pozostałe boki są niewiadomą. Oblicz pozostałe długości boków.
Rozwiązanie:
na początku należy sporządzić rysunek poglądowy:

Najpierw, z zależności funkcji trygonometrycznych, wyliczymy bok . Wykorzystamy – czyli stosunek przyprostokątnej leżącej naprzeciw kąta ostrego do przeciwprostokątnej.

Aby obliczyć długość boku wykorzystamy tangens 45°.

Odpowiedź: długości boków to i

Zadanie:
Drzewo, na które patrzy Janek ma wysokość 6 m. Janek stoi od drzewa w pewnej odległości. Pod kątem 45 stopni Janek patrzy na wierzchołek drzewa. Oblicz odległość Janka od wierzchołka drzewa.
Rozwiązanie: najpierw sporządzimy rysunek poglądowy:

Drzewo, czyli bok ma wysokość 6m. Kąt . Odległość Janka, czyli punktu od wierzchołka drzewa, to przeciwprostokątna naszego poglądowego trójkąta prostokątnego oznaczonego jako
Przy obliczeniach skorzystamy z , czyli z zależności przyprostokątnej znajdującej się naprzeciw kąta do przeciwprostokątnej.

|

Odpowiedź: Odległość Janka od wierzchołka drzewa wynosi .