Opracowanie:
Sin cos
Sin cos
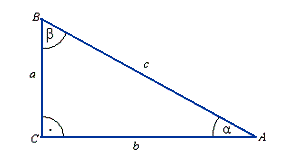
Sinus i cosinus to dwie z czterech funkcji trygonometrycznych. Na początku narysujmy sobie trójkąt prostokątny. W odpowiedni sposób porównując długości boków możemy otrzymać sinus bądź też cosinus.
Sinus kąta alfa określa się stosunkiem boku a do boku c, a więc przyprostokątnej naprzeciw kąta do przeciwprostokątnej.
Cosinus kąta alfa określa się stosunkiem boku b do boku c, a więc przyprostokątnej przy kącie do przeciwprostokątnej.
Dla kąta beta sinus i cosinus będzie wyglądać o tak:
Jak widzisz, jeśli kąt alfa i beta są ostre, i należą do jednego trójkąta prostokątnego zachodzi zależność:
Aby łatwo zapamiętać to, jak się oblicza sinus i cosinus spójrz na rysunki poniżej.
zadanie 1
Oblicz sinus oraz cosinus kąta alfa.
Rozwiązanie takiego zadania będzie bardzo proste. Wystarczy wypisać dane i odpowiednio je podstawić do wzorów.
zadanie 2
Podaj sinus i cosinus kąta ostrego zaznaczonego na rysunku.
Jak wiesz, aby obliczyć sinus i cosinus musimy znać długości wszystkich boków w trójkącie. W tym przypadku nie znamy długości przeciwprostokątnej. Jednakże obliczenie jej długości nie jest dla nas problemem. Wystarczy, że podstawimy odpowiednie dane do twierdzenia Pitagorasa i gotowe.
Oznaczmy nasz niewiadomy bok jako „c”
W takim razie:
W związku z tym, że w mianowniku pozostawał pierwiastek, usuwamy tę niewymierność poprzez sprzężenie, a więc poprzez rozszerzenie mianownika i licznika przez mianownik
Ponadto, z sinusem i cosinusem jest związanych kilka wzorów. Bardzo popularnym jest tak zwana jedynka trygonometryczna. Dla każdego kąta, zachodzi zależność:
Oczywiście, wzór ten można śmiało udowodnić.
Skoro następuje zależność: i , to (pamiętając o twierdzeniu Pitagorasa: ):
Ponadto, wykorzystując sinus i cosinus możemy otrzymać tangens lub też cotangens.
Wiemy, że tangens jest odwrotnością cotangensa, więc:
Podsumowując więc, znajomość co najmniej jednej wartości funkcji trygonometrycznej, pozwala nam na obliczenie wszystkich pozostałych funkcji.
zadanie
Oblicz sinus kąta alfa wiedząc, że
Aby rozwiązać te zadanie skorzystamy z jedynki trygonometrycznej.
zapisujemy równanie
podstawiamy dane i podnosimy do kwadratu dane wartości
przerzucamy wiadome na prawą stronę równania
obustronnie pierwiastkujemy
wyciągamy ostateczny wniosek
Odpowiedź: Sinus kąta alfa wynosi .
zadanie
Podaj sinus i cosinus zaznaczonego kąta ostrego.
Rozwiązanie takiego zadania zaczynamy od obliczenia długości przeciwprostokątnej. Jak widzisz, mamy trójkąt prostokątny, więc zastosujemy twierdzenie Pitagorasa. Nasz niewiadomy bok oznaczyłam literką c.
W takim razie przejdźmy do wyznaczania wartości:
Tutaj otrzymaliśmy na początku w mianowniku niewymierność (pierwiastek), dlatego zastosowaliśmy sprzężenie, aby usunąć tę niewymierność z mianownika.
Tutaj usunęliśmy w ten sam sposób jak powyżej niewymierność z mianownika.
Podsumowując więc, każdorazowo gdy znamy jedną wartość funkcji trygonometrycznej, a mamy obliczyć pozostałe, stosujemy jedną z dwóch metod.
Stosując twierdzenie Pitagorasa obliczamy poszczególne długości boków, a następnie podstawiamy je do definicji funkcji trygonometrycznych.
Zastosowanie jedynki trygonometrycznej oraz jednego ze wzorów na tangens czy też cotangens rozwiązuje nam zadanie.
To warto zapamiętać, gdyż bardzo często będziesz się spotykać właśnie z zadaniami, w których masz obliczyć pozostałe funkcje trygonometryczne, mając podaną wartość jednej z nich.
Oczywiście, możesz się także spotkać z innymi typami zadań. Każde jednak rozwiązujemy mniej więcej tą samą metodą. Szukamy takich boków/kątów, abyśmy mogli obliczyć dany bok/dany kąt/wartość danej funkcji.