Sinus 30

Zacznijmy od przypomnienia sobie czym jest sinus.
Sinus to stosunek przyprostokątnej leżącej naprzeciwko kąta, którego chcemy podać sinus do przeciwprostokątnej.
Nazwy przyprostokątna i przeciwprostokątna informują nas, że sin liczymy w trójkącie prostokątnym.
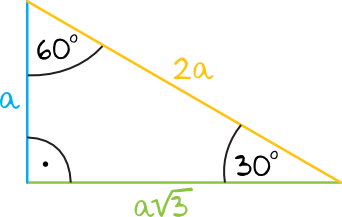
Sinus 30 możemy obliczyć w oparciu o trójkąt 30,60,90.
Przypomnijmy założenia między bokami w trójkątach 30,60,90.
Naprzeciwko kąta o największej mierze (90) leży najdłuższy bok (2a)
Naprzeciwko kąta o średniej mierze (60) leży bok o średniej długości (a)
Naprzeciwko najmniejszego kąta (30) leży najkrótszy bok (a)
Pokażmy na rysunku

Zgodnie z definicją obliczmy sin 30.
„Stosunek przyprostokątnej leżącej naprzeciwko kąta do przeciwprostokątnej”
Zatem sin30=
„a” możemy skrócić i zostaje nam
Sin kąta 30 zawsze ma wartość
Obliczmy wszystkie wartości funkcji trygonometrycznych dla kątów 30,60, a dowiemy się pewnych zależności.
Przypomnijmy definicje poszczególnych funkcji trygonometrycznych.
Sinus to stosunek długości przyprostokątnej leżącej naprzeciwko naszego kąta do długości przeciwprostokątnej.
Cosinus to stosunek długości przyprostokątnej leżącej przy naszym kącie (przylega do naszego kąta) do przeciwprostokątnej.
Tangens jest stosunkiem długości przyprostokątnej leżącej naprzeciwko naszego kąta do długości przyprostokątnej przylegającej do tego kąta.
Cotangens jest odwrotnością tangensa, więc jego definicja brzmi: Cotangens to stosunek długości przyprostokątnej przylegającej do naszego kąta do przyprostokątnej leżącej naprzeciwko tego kąta.
Znając definicję poszczególnych funkcji trygonometrycznych obliczmy ich wartości dla kątów 30 i 60.

Jak możemy zauważyć pojawiły nam się pewne zależności:

Zadanie 1.
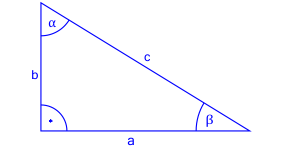
Oblicz wartości funkcji trygonometrycznych w trójkącie prostokątnym jeżeli wiesz, że przeciwprostokątna ma długość 14, bok a przyprostokątne mają długości 7 i 7.

Mamy podane długości boków możemy więc zapisać zgodnie z oznaczeniami na rysunku



Już tutaj możemy zorientować się, że trójkąt, który mamy podany w treści zadania to trójkąt o kątach 30,60,90.
Jeżeli naprzeciwko kąta 90 leży bok 2a, a w naszym przypadku wynosi on 14 to obliczmy jaką długość ma bok „a”, czyli ten leżący naprzeciwko kąta 30.
2a=14
a=7
Zatem bok, który ma długość 7 ( na naszym rysunku to ten, który leży naprzeciwko kąta ) to bok, który leży naprzeciwko kąta 30.
Co oznacza, że

W takim razie obliczmy kąt .





Mamy więc trójkąt 30,60,90.
Możemy skorzystać z wartości, które wyżej wyznaczaliśmy, ale jeśli ich nie pamiętamy to obliczmy wartości poszczególnych funkcji trygonometrycznych podstawiając długości boków.

Obliczmy więc wartości funkcji trygonometrycznych dla kąta 30.




Teraz obliczmy wartości funkcji trygonometrycznych dla kąta 60.

Wartości funkcji trygonometrycznych po podstawieniu długości poszczególnych boków zgadzają się z tymi, które wcześniej obliczyliśmy ogólnie, bez konkretnych boków.

Zadanie 2
Oblicz pole trójkąta mając podane długości dwóch boków a=6 b=9, a także kąt między dwoma tymi bokami, który ma miarę 60.
Przypomnijmy wzór na pole trójkąta w, którym możemy wykorzystać dane, które mamy w zadaniu.

Wzór mówi, że pole trójkąta to połowa iloczynu boków i sinusa kąta zawartego między nimi.
Podstawmy zatem dane z naszego zadania.

Wiemy, że

Zadanie 3.
Oblicz tangens kąta ostrego , jeżeli wiesz, że kąt ten ma miarę 30.
Tutaj rozszerzymy trochę naszą wiedzę i uzupełnimy o dodatkowe informacje.
Przypomnijmy sobie wzór na tangens kąta.

Wiemy, że kąt ma miarę 30 stopni.
W tym zadaniu ważne jest żebyśmy pamiętali chociaż jedną wartość funkcji. Jeżeli pamiętamy wartość tg to całe zadanie mamy zrobione.
Co jeśli nie pamiętamy ani tangensa, ani jego odwrotność czyli cotangens?
Najłatwiej zapamiętać , bo jest to .
Skorzystajmy z tej wiedzy.
Mamy podany sinus, ale nie mamy cosinusa. Jak go zatem obliczyć?
Musimy przypomnieć wzór tzw. jedynki trygonometrycznej.

Suma kwadratów sinusa i cosinusa tego samego kąta zawsze jest równa 1.
Jeżeli znamy sin to obliczmy z tego wzoru cos.





Spierwiastkujmy.
lub
W naszym przypadku kąt ma miarę 30 stopni, zatem jest kątem ostrym. Dla kąta ostrego wszystkie wartości funkcji trygonometrycznych są dodatnie. Odrzucamy zatem drugą opcję.

Jeżeli mamy już obliczony sin i cos możemy obliczyć tg.




Dzielenie dwóch ułamków możemy zmienić na mnożenie pierwszego przez odwrotność drugiego.


Warto jest zatem zapamiętać wartości funkcji trygonometrycznych kątów z tzw. charakterystycznych trójkątów tj. 30, 60 i 45.
Znając tg 30 stopni moglibyśmy od razu podać odpowiedź, zamiast wszystko wyliczać.
Zamieszczę Wam tabelkę, którą warto nauczyć się na pamięć, ponieważ umożliwi nam to szybsze rozwiązywanie zadań.

Jeżeli przypomnieliśmy już tzw. jedynkę trygonometryczną możemy rozwiązać zadanie w którym użycie jej będzie niezbędne.
Uważam, że jest ona w trygonometrii niezwykle ważna, więc przy okazji tematu trygonometrii możemy ją poćwiczyć, ale żeby nie odbiegać od naszego tematu rozwiążemy z nią tylko jedno zadanie.

Zadanie 4.
Kąt jest ostry i spełniona jest nierówność . Oblicz wartości , a następnie pozostałych wartości funkcji trygonometrycznych.
Zawsze, gdy w zadaniu mamy podany sin i trzeba obliczyć cos tego samego kąta korzystamy z jedynki trygonometrycznej:
Mamy podany sin, zatem podstawmy do wzoru:





Pierwiastkujemy.
lub
W treści zadania podane mamy, że kąt jest ostry ( dla kąta ostrego wszystkie wartości funkcji trygonometrycznych są dodatnie). Odrzucamy zatem drugą możliwość.

Znając sinus i cosinus możemy obliczyć tangens korzystając z wzoru




Znając tangensa możemy obliczyć wartość cotangensa. Wiemy, że cotangens to odwrotność tangensa, więc cotangens możemy obliczyć z wzoru:




Obliczyliśmy wartości wszystkich funkcji trygonometrycznych ćwicząc przy okazji tzw. jedynkę trygonometryczną.