Sinus cosinus tangens

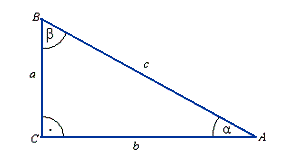
Zajmiemy się dziś trzema z czterech funkcji trygonometrycznych. Narysujmy trójkąt prostokątny. Oznaczmy jego wierzchołki literami. Przyjmijmy, że bok naprzeciw wierzchołka A będzie bokiem a, bok naprzeciw wierzchołka B będzie bokiem b itd.

Jeśli w odpowiedni sposób zapiszemy stosunki odpowiednich długości boków, to otrzymamy definicje funkcji trygonometrycznych w trójkącie prostokątnych.

Zauważ, że w trójkącie równobocznym te funkcje są ze sobą ściśle powiązane. Stosunek boku a (przyprostokątnej naprzeciw kąta) oraz boku c (przeciwprostokątnej) względem kąta afla jest równy co do wartości stosunku długości boku a do boku c względem kąta .

Oczywiście, skoro jest mowa o funkcjach trygonometrycznych, to jak na każdą funkcje przystało, możemy naszkicować jej wykres.

Sinusoida, a więc wykres funkcji sinus przedstawia się następująco:

Cosinusoida, a więc wykres funkcji cosinus przedstawia się następująco:

Tangensoida, a więc wykres funkcji tangens przedstawia się następująco:

Z wyżej pokazanych wykresów możemy korzystać, gdy chcemy odczytać wartość danej funkcji. Mimo to, zaleca się korzystanie z tablic trygonometrycznych, które ułatwiają nam odczytanie wartości. Tym samym, mamy większą pewność, że nie popełniliśmy błędu w odczytywaniu wartości z wykresu.

zadanie 1
Oblicz sinus, cosinus oraz tangens kąta alfa dla poniższego rysunku.

Rozwiązanie:
Zacznijmy od sinusa. Robimy stosunek długości przyprostokątnej naprzeciw kąta do przeciwprostokątnej.

Teraz czas na cosinusa. Robimy stosunek długości przyprostokątnej przy kącie do przeciwprostokątnej.

Na koniec powiedzmy sobie o tangensie. Porównujemy długość przyprostokątnej naprzeciw kąta do przyprostokątnej przy kącie.

zadanie 2
Podaj wartości sinusa, cosinusa oraz tangensa dla zaznaczonego kąta.

Jak widzisz, nie mamy podanej długości przeciwprostokątnej. Obliczymy ją stosując twierdzenie Pitagorasa.

Zapisujemy równanie

Podnosimy wartości do kwadratu

Dodajemy do siebie wartości oraz obustronnie pierwiastkujemy

Otrzymujemy wynik

Teraz przechodzimy do obliczania wartości funkcji trygonometrycznych.

zadanie 3
Dane jest, że cosinus kąta ostrego alfa w trójkącie prostokątnym wynosi . Oblicz sinus tego kąta.

I sposób rozwiązania

W trygonometrii wyróżniamy kilka wzorów, które pozwalają nam obliczać wartości trygonometryczne. Jednym z najbardziej popularnych wzorów jest jedynka trygonometryczna, która wygląda następująco:

U nas wiadomy jest cosinus, więc podstawiamy go do naszego równania. Następnie przekształcamy je, aby wyliczyć sinusa.

Podstawiamy dane, a następnie przerzucamy wiadome na prawą stronę.

Odejmujemy do siebie wartości po prawej stronie.

Obustronnie pierwiastkujemy.

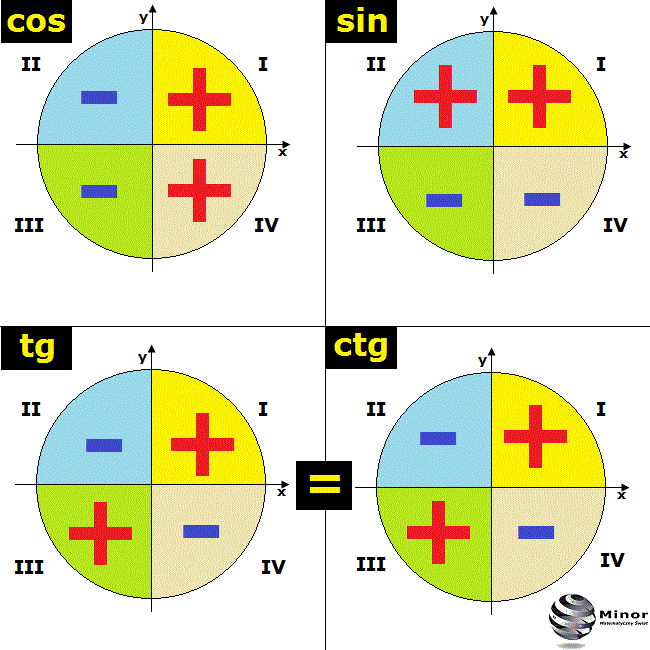
W związku z tym, że kąt alfa jest ostry, znajdujemy się w pierwszej ćwiartce układu współrzędnych. Tym samym wartości trygonometryczne są tam dodatnie.

II sposób rozwiązania

Oczywiście, mogliśmy jeszcze rozwiązać te zadanie rysując trójkąt prostokątny. Poprzez obliczenie przyprostokątnej naprzeciw kąta z twierdzenia Pitagorasa, bez problemu obliczylibyśmy sinus kąta alfa.

Założenia:
a > 0

Rozwiązanie:

Przerzucamy wiadome na prawą stronę

Odejmujemy od siebie odpowiednie wartości

Obustronnie pierwiastkujemy

Otrzymujemy wynik.

Z tego rysunku odczytujemy, że