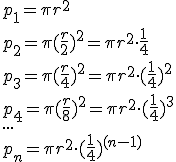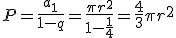Opracowanie:
Suma szeregu geometrycznego

Suma szeregu geometrycznego

Zweryfikowane

Suma szeregu geometrycznego to szereg postaci :

{displaystyle sum _{n=1}^{infty }aq^{n-1};{}} gdzie:

,a’ pierwszym wyrazem szeregu geometrycznego
,q’ – ilorazem szeregu geometrycznego
,n’ – tą sumą częściową jest suma pierwszych ,n’ wyrazów szeregów :

{displaystyle S_{n}=a+aq+...+aq^{n-1}=sum _{k=1}^{n}aq^{k-1},quad nin mathbb {N} .}

Jest jeszcze twierdzenie dotyczące szeregu geometrycznego:
szereg geometryczny jest zbieżny, gdy /q/< 1 i ma sumę: S=lim_{ntoinfty}S_n=lim_{ntoinfty}(a_1cdot frac{1-q^n}{1-q})=lim_{ntoinfty}[frac{a_1}{1-q}cdot (1-q^n)]=\=lim_{ntoinfty}(frac{a_1}{1-q}-frac{a_1}{1-q}q^n)=frac{a_1}{1-q}-frac{a_1}{1-q}cdot{lim_{ntoinfty}(q^n)}=frac{a_1}{1-q}-0=frac{a_1}{1-q}

Co w skrócie można przedstawić w postaci (który jest wykorzystywany częściej):

dodatkowo jest rozbieżny gdy |q| 1

W tym przypadku założyliśmy, że /q/< 1 , gdyż jedynie w takim przypadku: 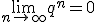lim_{ntoinfty}q^n=0 ||| W przeciwnym (w innym) przypadku granica ta jest nieskończona (czyli niewłaściwa) i suma szeregu również jest nieskończona.

Do czego nam się to może przydać?
Możemy to wykorzystać do zamieniania liczb nieskończonych okresowych na ułamek lub do obliczania pola powierzchni nieskończonej liczby figur, długości nieskończonej liczby odcinków, albo objętości nieskończonej ilości brył, ale tylko spełnione są odpowiednie warunki. Może się zdarzyć nawet, że wartości te wcale nie są nieskończone.

Zad. 1
Zamień liczbę 0,(7) na ułamek zwykły.

Można zauważyć, że:
0,(7)= 0,7777…=

Mamy więc szereg geometryczny o ilorazie q=0,1 ||| a1=0,7 , a więc: sumując wszystkie wyrazy szeregu otrzymujemy wynik równy:

Zad. 2

W środku koła o promieniu ,r’ rysujemy koło o promieniu o połowę krótszym. W środku mniejszego koła rysujemy koło, którego promień również jest o połowę mniejszy (ale od koła w które jest wpisane- najbliższe koło o większym promieniu) i tak dalej. Oblicz pole powierzchni wszystkich kół.

Uwaga:
Nie daj się nabrać i przypadkiem nie obliczyć pola jednego koła jako wszystkich, w tym przypadku liczymy sumę pól kolejnych kół ,,nakładanych” na siebie (czyli wszystkich z osobna).

Rozwiązanie:
Zróbmy sobie rysunek pomocniczy: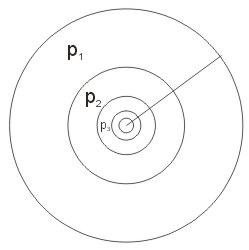
koła współśrodkowe - przykłąd sumy szeregi geometrycznego
Wypiszmy sobie pola poszczególnych kół:

p_1=pi{r^2}\p_2=pi{(frac{r}{2})^2}=pi{r^2}cdot{frac{1}{4}}\p_3=pi{(frac{r}{4})^2}=pi{r^2}cdot{(frac{1}{4})^2}\p_4=pi(frac{r}{8})^2=pi{r^2}cdot(frac{1}{4})^3\...\p_n=pi{r^2}cdot(frac{1}{4})^{(n-1)}

Więc łączne pole wszystkich kół wynosi:

Więc szereg geometryczny wynosi:
a1= πr2
q=

mamy spełniony warunek zbieżności szeregu geometrycznego, więc możemy obliczyć sumę (czyli pole) wszystkich figur:

P=frac{a_1}{1-q}=frac{pi{r^2}}{1-frac{1}{4}}=frac{4}{3}pi{r^2}

Koniec

Powyższe zadanie zostało zweryfikowane przez nauczyciela
To top