Sześciokąt foremny

Dzisiaj zagłębimy się w świat geometrii. Poznasz szczególny przypadek sześciokąta oraz dowiesz się o jego przekątnych, powierzchni, obwodzie, wysokości, bokach itd.

Na początku wyjaśnijmy sobie czym jest sześciokąt. Innymi nazwami dla tej figury jest również sześciobok oraz heksagon.

Generalnie rzecz ujmując, każda figura płaska, która składa się z sześciu boków oraz z sześciu kątów wewnętrznych stanowi sześciokąt. Ponadto należy pamiętać, że w każdym sześciokącie suma miar kątów wewnętrznych wynosi 720°. W takim razie, miary poszczególnych kątów mogą mieć różne miary. My skupimy się jednak na tym, który posiada wszystkie tej samej miary kąty wewnętrzne. W takim razie o takim sześciokącie, którego wszystkie miary kątów są takie same, a więc tym samym boki są tej samej długości, mówimy, że jest on sześciokątem foremnym.

Skoro już wiemy ile wynosi suma miar kątów w tej figurze, to spróbujmy policzyć jaką miarę ma kąt wewnętrzny sześciokąta foremnego.

Kąt wewnętrzny sześciokąta foremnego wynosi 120°.

W związku z tym, że między miarą łukową kąta, a miarą kąta występuje pewna zależność, możemy te 120 stopni przedstawić też w innej postaci. Aby przeliczyć tę zależność można użyć proporcji. W pierwszym wierszu wpisujemy nasze „dane”, którymi jest równość 180 stopni oraz pi radianów.
180°—>π rad
120°—>x

Kąt wewnętrzny sześciokąta foremnego wynosi .

Teraz powiemy sobie coś o tym, jak narysować tę figurę. Oczywiście zawsze możemy użyć jakiś matematycznych szablonów, w których znajdziemy szukaną przez nas figurę. Jeśli mamy kartkę w kratkę oraz ołówek i linijkę to jesteśmy w stanie bez większego problemu narysować sześciokąt o bokach tej samej długości. Jeśli jednak nie mamy ani kartki w kratkę, możemy użyć tego troszke trudniejszego sposobu rysowania, a raczej konstruowania sześciokąta foremnego.

Zaczynamy od przygotowania kartki oraz cyrkla, linijki oraz ołówka.
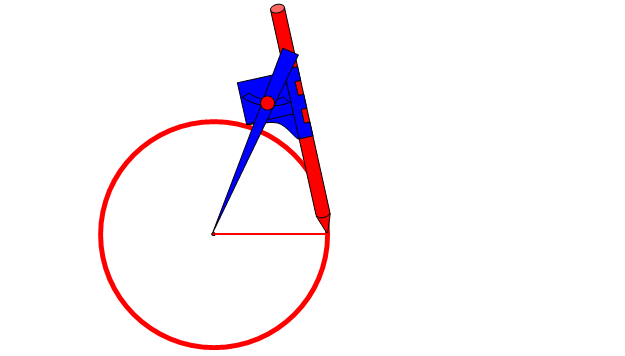
Na kartce rysujemy okrąg. W tym momencie pojawia się pewnie pytanie: „Na jaką rozwartość cyrkla mam narysować ten okrąg?”. Generalnie rzecz biorąc, twoja rozwartość cyrkla będzie stanowić połowę długości przekątnej otrzymanego sześciokąta foremnego
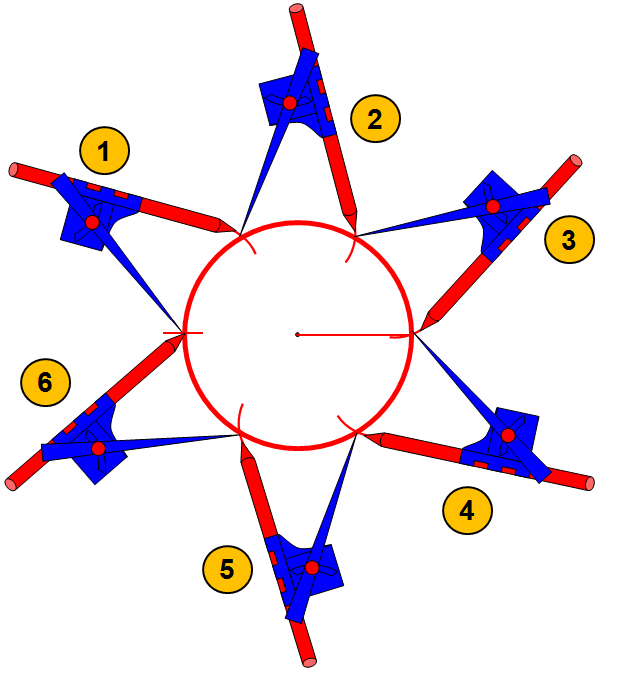
Co ważne, nie zamykaj cyrkla. Nadal miej zachowaną rozwartość cyrkla, którą był rysowany okrąg. Następnie postępuj tak jak na rysunku poniżej. Wybierz dowolny punkt na okręgu. Wbij do niego cyrkiel i częścią rysującą zaznacz przecięcie na okręgu. Kolejno w miejsce przecięcia się okręgu z powstałym łukiem wbij kolejny raz cyrkiel i tą samą rozwartością cyrkla narysuj kolejny mini łuk. Postępuj tak do zaznaczenia łącznie sześciu mniejszych łuków.
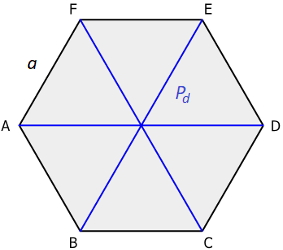
Następnie połącz ze sobą punkty przy pomocy linijki. Punkt jeden z punktem dwa, punkt dwa z punktem trzy itd. Podczas rozwiązywania zadań z matematyki warto również narysować sobie przekątne tej figury. Przekątne utworzymy poprzez połączenie punktu 1 i 4, punktu 2 i 5 oraz poprzez połączenie punktu 3 i 6.
Zauważ co powstało po dodaniu przekątnych.

Teraz spójrzmy na kąty. Kąt CBA ma miarę 120°. Po narysowaniu przekątnych powstało nam sześć trójkątów. Teraz spróbujmy określić, jakie te trójkąty są. Podzielmy kąt 120° na dwa, gdyż przekątna podzieliła ten kąt na dwa mniejsze takie same kąty.

Taka sama sytuacja będzie w pozostałych kątach. Oznacza to więc, że miary kątów przy podstawie trójkątów wynoszą po 60°. Pamiętając, że trójkąt ma 180°, możemy obliczyć jaki kąt tworzy się przy przecięciu przekątnych.
180° – 60° – 60° = 60°
Tym samym możemy powiedzieć, że w każdym z powstałych trójkątów kąty wynoszą po 60°. Oznacza to więc, że boki powstałych trójkątów są takie same, a więc powstałe trójkąty to trójkąty równoboczne. Poniżej przedstawię kilka wzorów, które na pewno przydadzą się podczas rozwiązywania zadań matematycznych. Aby obliczyć wysokość w trójkącie równobocznym oprócz możliwości użycia np. wzoru na pole trójkąta, a następnie przekształcenia go, jest możliwość użycia specjalnego wzoru, który sprawdzi się tylko dla trójkątów równobocznych: . Niewiadoma a jest bokiem trójkąta i tym samym bokiem sześciokąta, z którego powstał.

Jeśli natomiast musimy obliczyć pole takiego jednego trójkącika możemy użyć wzoru na pole trójkąta równobocznego: . Niewiadoma a jest bokiem trójkąta i tym samym bokiem sześciokąta, z którego powstał.

W związku z tym, że wiemy, że każdy sześciokąt foremny składa się z sześciu takich trójkątów, wzór na pole sześciokąta możemy wyrazić jako pomnożony przez sześć wzór na pole trójkąta równobocznego: . Oczywiście, szóstkę oraz czwóreczkę możemy skrócić, lecz często w zadaniach są takie dane, że lepiej jest aby nie skracać tych wartości od razu.

Zważywszy na to, że boki tej figury są takie same, wzór na obwód takiej figury jest bardzo prosty, gdyż stanowi on sumę długości wszystkich boków, a więc:

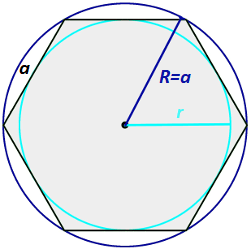
Gdybyśmy mieli podany sześciokąt, który jest wpisany w okrąg (figury mają ten sam środek) to aby obliczyć długość promienia okręgu wpisanego w sześciokąt foremny powinniśmy użyć wzoru:

Ponadto warto wspomnieć, że jeżeli chcemy mówić o długości promienia okręgu opisanego, to mówimy tutaj o boku a, więc są one równe co do swojej długości: R = a
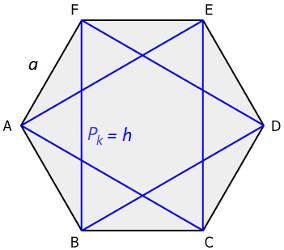
Aby obliczyć długość dłuższej przekątnej sześciokąta foremnego wystarczy jeszcze raz spojrzeć na rysunek, na którym przedstawiony jest sześciokąt podzielony na trójkąty równobocznego. Na podstawie tego możemy pokazać wzór na długość dłuższej przekątnej(na rysunku ): 2a=2R

Jeżeli chcemy obliczyć długość krótszej przekątnej sześciokąta foremnego powinniśmy użyć wzoru na długość krótszej przekątnej (na rysunku h):

Skoro poznaliśmy już najważniejsze wzory i zagadnienia, z którymi możemy spotkać się w życiu codziennym, spróbujmy rozwiązać zadanie.

Zadanie 1
Oblicz obwód sześciokąta foremnego wiedząc, że pole jego wynosi .

Najpierw ustalmy co jest naszą niewiadomą. Szukaną przez nas jest obwód, który wynosi sześć razy bok naszej figury. Tym samym możemy przyrównać podane pole do wzoru na pole sześciokąta foremnego. Następnie możemy przekształcić wzór i wyliczyć a, które na koniec podstawimy do wzoru na obwód. Ponadto przypominam, że TRZEBA PAMIĘTAĆ O ZAŁOŻENIACH. Długość boku nie może być ujemna.
a>0

obustronnie dziele przez pierwiastek z trzech.


odrzucamy drugi wynik gdyż jest sprzeczny z założeniem, a następnie prawidłowy wynik rozszerzamy, aby mieć lepszą postać wyniku


Odpowiedź: Obwód wynosi .