Tanges

Zacznijmy od przypomnienia czym jest tangens.
Tangens jest to jedna z funkcji trygonometrycznych, której definicja brzmi:
Tangens to stosunek długości przyprostokątnej leżącej naprzeciwko kąta z, którego chcemy wyliczyć tangens do długości przyprostokątnej przylegającej do tego kąta.
Przypomnijmy, że przyprostokątne znajdują się w trójkącie prostokątnym przy kącie prostym, czyli . Natomiast przeciwprostokątna leży naprzeciwko tego kąta.
Tangens jest odwrotnością cotangensa.
Zgodnie z oznaczeniami na poniższym rysunku podajmy wartość tangensa.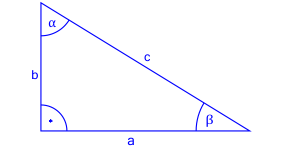



Kiedy tangens jest dodatni a kiedy ujemny?
Tangens jest dodatni dla kątów:
Od do .
Od do .
Z tego wynika, że tangens jest ujemny dla kątów:
Od do .
Od do .
Poćwiczmy podawanie tangensa dla różnych kątów.
Ćwiczenie 1.
Podaj wartości tangensa oraz cotangensa dla kątów zaznaczonych na poniższych rysunkach.
a)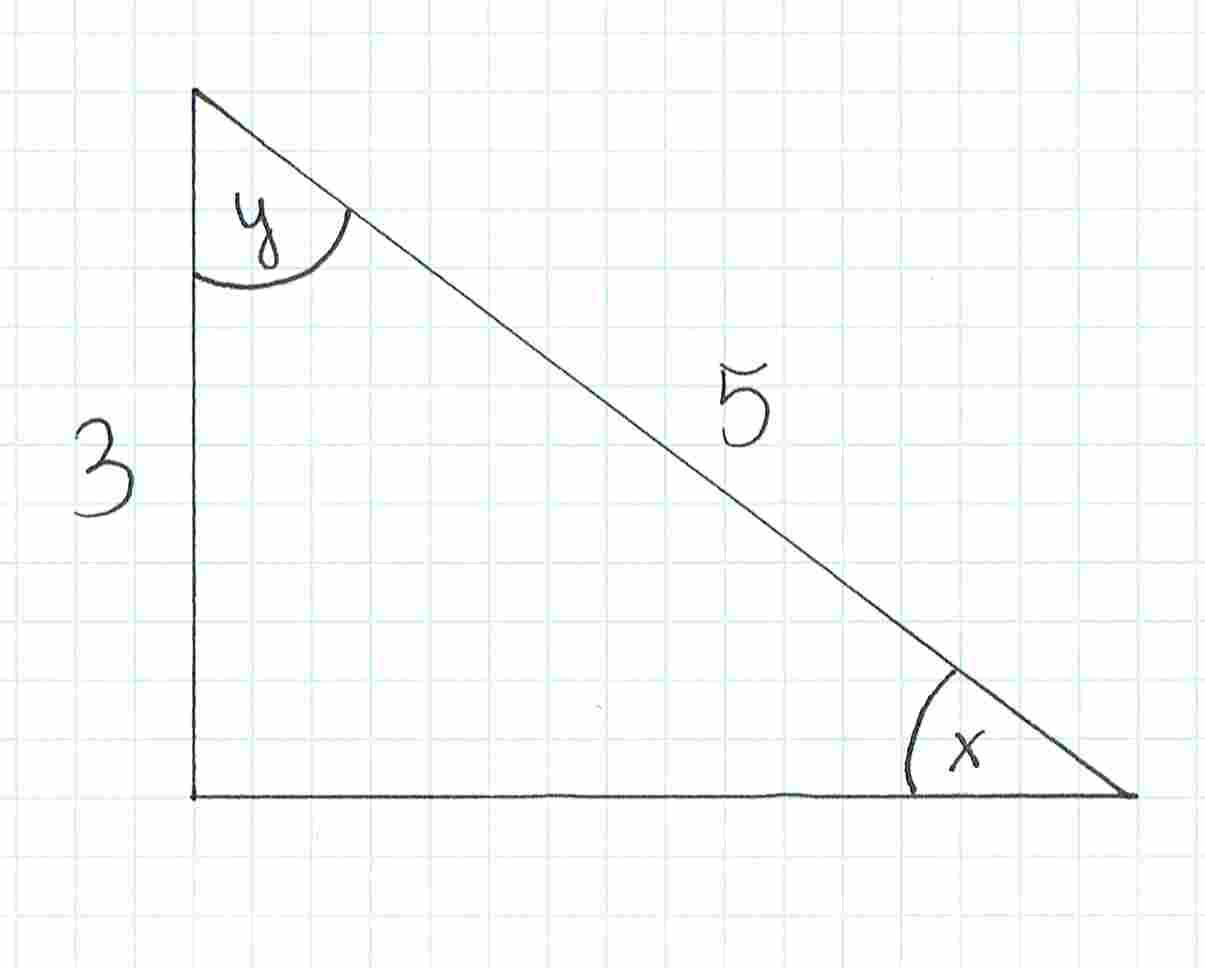

Wiemy, że żeby obliczyć tangens potrzebujemy przyprostokątnych. (skoro cotangens to odwrotność tangensa to wystarczy tylko zamienić kolejność, więc do obliczenia cotangensa również potrzebujemy przyprostokątnych).
Na rysunku mamy zaznaczoną jedną przyprostokątną, a także przeciwprostokątną, także potrzebujemy obliczyć długość drugiej przyprostokątnej. Możemy to zrobić korzystając z Twierdzenia Pitagorasa. Przypomnijmy zatem jego treść.
Twierdzenie Pitagorasa:
Jedna przyprostokątna podniesiona do kwadratu (do potęgi drugiej) po dodaniu do kwadratu drugiej przyprostokątnej daje nam kwadrat przeciwprostokątnej.
Przyjmijmy oznaczenia i zapiszmy to twierdzenie na literkach. (a i b to przyprostokątne, c to przeciwprostokątna)

Korzystając zatem z tego twierdzenia obliczmy długość drugiej przyprostokątnej. Oznaczmy jej długość jako „a”.



Przenieśmy 9 na prawą stronę równania, pamiętając o zmianie znaku.


Spierwiastkujmy obie strony.
lub
Drugą opcję odrzucamy, ponieważ bok trójkąta nie może być ujemny, zatem druga przyprostokątna ma długość 4.
Mamy już długości przyprostokątnych.
Zacznijmy od obliczenia tangensa kąta y.
Jest to stosunek przyprostokątnej leżącej naprzeciwko do tej, która przylega do kąta.

Cotangens to odwrotność tangensa zatem wystarczy zamienić miejsca.

Obliczmy teraz wartości dla kąta „x”.

Zatem cotangens to odwrotność, więc:

Możemy zauważyć pewne zależności z tymi wartościami:

b)

W tym przypadku mamy podobną sytuację. Mamy podaną przyprostokątną oraz przeciwprostokątną . Naszym zadaniem jest obliczyć długość przyprostokątnej .
Skorzystajmy z Twierdzenia Pitagorasa:

Podstawmy nasze dane z zadania:

Podnieśmy liczby do kwadratu ( do drugiej potęgi).

Przenieśmy 81 na drugą stronę równania pamiętając o tym, że przy przenoszeniu zmieniamy znak.


Teraz spierwiastkujmy żeby otrzymać długość odcinka .

Mamy już obliczone długości przyprostokątnych więc możemy obliczyć tangens i cotangens obu kątów ostrych w tym trójkącie.
Przypomnijmy, że nazywając kąty to środkowa literka jest ta, przy której kąt jest położony.
Zatem na rysunku mamy kąt oraz kąt .

Kąt leży przy wierzchołku B i od niego zacznijmy.

Możemy usunąć niewymierność z mianownika.

Cotangens jest odwrotnością tangensa więc:

Mamy już obliczany tangens i cotangens dla kąta przy wierzchołku B, więc obliczmy tangens i cotangens dla kąta przy wierzchołku A.

Więc jeżeli cotangens to odwrotność to:

Znamy również dwa charakterystyczne trójkąty.
Pierwszy z nich to trójkąt o kątach , , , natomiast drugi to trójkąt o kątach .
Przypomnijmy zależności w takich trójkątach i obliczmy tangens.

Zacznijmy od trójkąta .
Przypomnijmy zależności między bokami:
Naprzeciwko kąta najmniejszego (kąt o mierze 30o) leży najkrótszy bok (a).
Naprzeciwko kąta o średniej mierze (kąt 60o) leży bok o średniej długości (a).
Naprzeciwko kąta największego (kąt o mierze 900) leży najdłuższy bok (2a).
Przedstawmy te zależności na rysunku:

Obliczmy zatem tangens kątów ostrych, czyli o mierze

Drugi trójkąt to trójkąt o kątach .
Zależności między bokami w takim trójkącie wynikają z podzielenia kwadratu na dwa trójkąty wzdłuż przekątnej, której długość wynosi .
Przypomnijmy zasady dotyczące boków leżących naprzeciwko konkretnych kątów.
Naprzeciwko kątów, które mają mniejszą miarę (kąty 45o) leży bok a (krótszy bok).
Naprzeciwko kąta prostego (90o) leży bok dłuższy (pochodzi od przekątnej trójkąta)- .
Przedstawmy takie zależności na rysunku, a także obliczmy tangens kąta .



Z wartości funkcji dla kątów, które obliczyliśmy możemy stworzyć tabelkę, której proponuję Wam się nauczyć, ponieważ te kąty często występują w zadaniach i można wpisać wartości ich funkcji trygonometrycznych bez obliczania każdej z nich.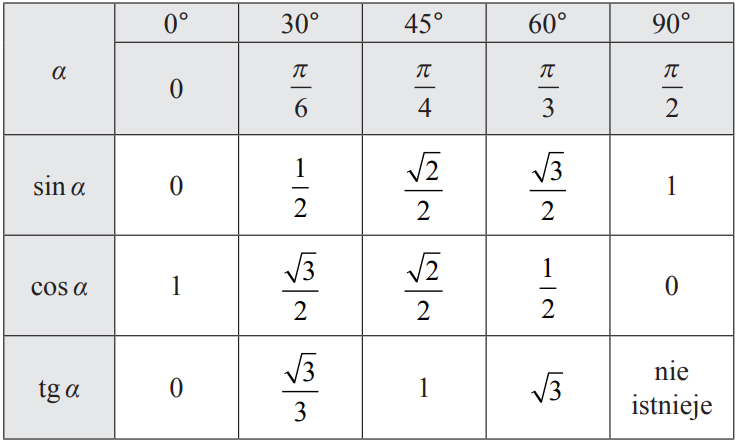

Niekiedy może się zdarzyć tak, że w zadaniu nie będziemy mieć podanego trójkąta, a wartość funkcji trygonometrycznej.
Jak zatem znaleźć inną funkcję trygonometryczną?
Gdy będzie to cotangens to nie mamy z tym problemu, ponieważ .
Co w przypadku, gdy będzie to sinus lub cosinus?
Musimy zacząć od przypomnienia definicji tych funkcji.
Sinus kąta to stosunek długości przyprostokątnej leżącej naprzeciwko kąta, z którego liczymy sinus do długości przeciwprostokątnej.
Cosinus kąta to stosunek długości przyprostokątnej leżącej przy tym kącie (przylega do tego kąta) do długości przeciwprostokątnej.
Ważnym wzorem w takich zadaniach jest wzór tzw. „jedynki trygonometrycznej”.

Wzór ten działa dla wszystkich kątów, więc znając sinus jakiegoś kąta możemy obliczyć jego cosinus i odwrotnie, gdy znamy cosinus kąta możemy obliczyć jego sinus.
Wzór na tangens z wykorzystaniem sinusa i cosinusa to .
Pokażmy wykorzystanie tej znajomości w zadaniach.

Ćwiczenie.
Oblicz tangens oraz cotangens kąta ostrego jeśli wiesz, że:
a)
b)
Zacznijmy od podpunktu a.
Zawsze, gdy w zadaniu mamy podany sinus lub cosinus i trzeba wyznaczyć jakąś inną funkcję trygonometryczną korzystamy z „jedynki trygonometrycznej”.
a) Jeżeli wiemy, że korzystając z jedynki trygonometrycznej obliczmy cosinus tego kąta.






lub
W naszym przypadku ( w treści zadania mamy podane, że kąt jest ostry), cosinus jest dodatni.
Odrzucamy zatem drugą opcję, więc .
Znamy już sinus i cosinus, więc możemy podstawić do wzoru na tangens.

Podpunkt b.
Działamy w ten sam sposób, tylko w „jedynkę trygonometryczną” wartość wstawiamy pod cosinusa.

lub
Drugą opcję odrzucamy, ponieważ kąt jest ostry, więc wszystkie funkcje trygonometryczne mają wartości dodatnie.

Możemy mieć również sytuację odwrotną. Możemy mieć podany tangens, a naszym zadaniem będzie obliczyć wszystkie pozostałe funkcje trygonometryczne.
W takim przypadku również będziemy korzystać ze wzoru: oraz z „jedynki trygonometrycznej”

Ćwiczenie
Oblicz wartości wszystkich funkcji trygonometrycznych kąta ostrego wiedząc, że:
a)
b)
Podpunkt a.
Wiemy, że

Wymnóżmy na krzyż

W jedynce trygonometrycznej podstawmy w miejsce cosinusa 4 sinusy.





lub
Drugi przypadek odrzucamy, ponieważ wiemy z treści zadania, że kąt jest ostry, więc sinus, jak i wszystkie inne funkcje trygonometryczne są dodatnie.
Usuńmy niewymierność z mianownika.

Mnożymy razy ułamek, który zarówno w liczniku, jak i w mianowniku ma pierwiastek z naszego wyjściowego mianownika.


Wiemy, że , ponieważ wyznaczyliśmy to sobie ze wzoru.
Podstawmy sinus i podajmy wartość cosinusa.

W treści zadania mieliśmy podany tangens, obliczyliśmy cosinus i sinus, więc wystarczy zebrać wszystko w jedno miejsce i zapisać.

Podpunkt b.
Wiemy, że , zatem możemy od razu podać cotangens .
Skorzystajmy z wzoru na tangens z użyciem sinusa i cosinusa.


Podstawmy do jedynki trygonometrycznej.





lub
W przypadku naszego zadania (w treści mamy podane, że kąt jest ostry) odrzucamy cosinus ujemny.

Usuńmy niewymierność z mianownika.


Obliczmy sinus tego kąta.



Zbierzmy teraz wszystkie wartości trygonometryczne do tego podpunktu.

Może zdarzyć się tak, że naszym zadaniem będzie obliczyć tangens lub bliźniaczy do niego cotangens z kąta, który będzie zaznaczony w układzie współrzędnych.
Pokażmy na przykładzie jak będziemy działać, a potem poćwiczymy.
W układzie współrzędnych kąt ma zawsze ramię początkowe nałożone na dodatnią część osi X, natomiast ramię końcowe jest ruchome i zależy od miary kąta.
Które kąty gdzie będą leżeć? Przypomnijmy podział układu współrzędnych na ćwiartki, z którego będziemy mogli podać w jakim przedziale znajduje się dany kąt.

Mamy cztery ćwiartki, które dzielą nam kąt pełny na 4 części, każda po 900, bo , zatem możemy zapisać w której ćwiartce znajdują się jakie kąty.
W ćwiartce pierwszej znajdują się kąty, których miara zawiera się w przedziale: od 0o do 90o.
W ćwiartce drugiej znajdują się kąty, których miara mieści się w przedziale: od 90o do 180o.
W ćwiartce trzeciej znajdują się kąty, których miara mieści się w przedziale: od 180o do 270o.
W ćwiartce czwartej znajdują się kąty, których miara mieści się w przedziale: od 270o do 360o.
Pokażmy zatem jak wygląda kąt w układzie współrzędnych.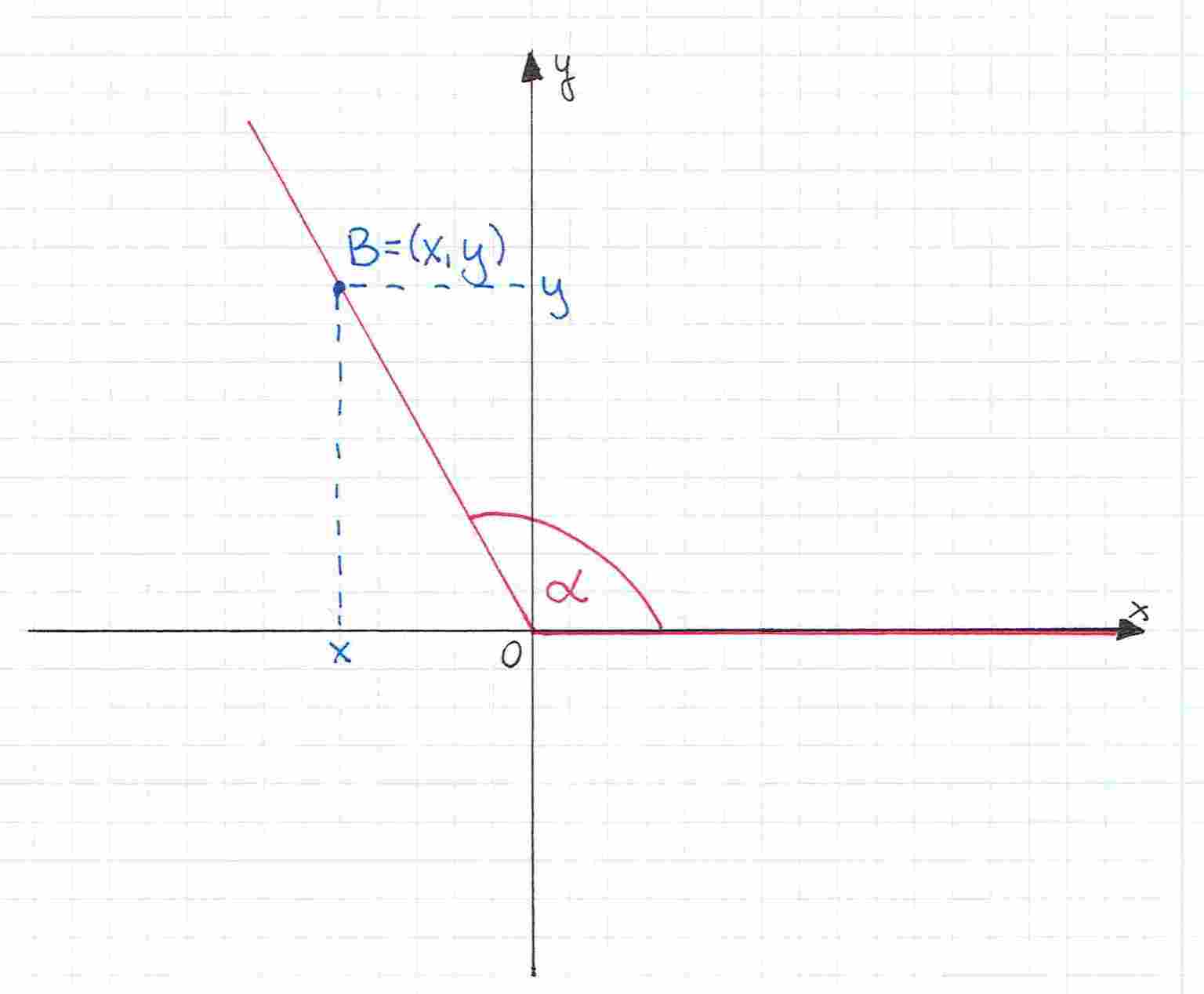

Żeby obliczyć wartości funkcji trygonometrycznych potrzebujemy znać współrzędne punktu, który leży na ramieniu końcowym tego kąta.
Gdy chcemy obliczyć tangensa będzie to: , więc jeżeli cotangens to odwrotność tangensa to: .

Zadanie.
Podaj wartości tangensa i cotangensa oraz podaj z jakiego przedziału jest kąt zaznaczony na rysunku.
a)
b)

Zacznijmy od podpunktu A.

Na wstępie odczytajmy współrzędne punktu P(x,y). (Pierwszą współrzędną odczytujemy z poziomej osi X, natomiast drugą odczytujemy z osi pionowej Y).

Zatem nasze x=-4, a y=5.

Obliczmy tangens.

Cotangens to odwrotność tangensa więc:

Ramię końcowe kąta leży w drugiej ćwiartce układu współrzędnych, więc kąt ma miarę od do .

Przejdźmy teraz do podpunktu B.
W tym przypadku również musimy odczytać współrzędne punktu A, który leży na końcowym ramieniu tego kąta.
Kierujemy się tą samą zasadą w odczytywaniu (zawsze w ten sposób odczytujemy współrzędne punktu).

Korzystamy z wzoru na tangens.

Cotangens to odwrotność tangensa zatem:

Ramię końcowe kąta którego mieliśmy obliczyć tangens i cotangens leży w drugiej ćwiartce układu współrzędny, więc w tym przypadku kąt również jak w podpunkcie wyżej ma miarę od do .

Mam nadzieję, że dobrze zrozumieliście ten temat i nie sprawi on Wam problemów, jednak żeby osiągnąć zamierzony efekt trzeba ćwiczyć to na przykładach.