Tg 30 stopni

Zacznijmy od przypomnienia czym jest tg, czyli tangens i jak brzmi jego definicja.

Tangens kąta to stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przyprostokątnej leżącej przy tym kącie, czyli przylegającej do niego.
Przedstawmy to na rysunku.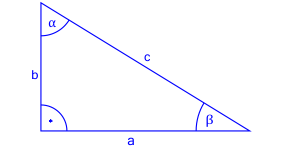

Korzystając z definicji podajmy wartość tangensa dla kąta oraz dla kąta .

W dzisiejszym opracowaniu mamy zająć się tangensem kąta o mierze .
Jego wartość możemy obliczyć korzystając z trójkąta charakterystycznego o kątach mających miarę .
Musimy przypomnieć lub dla niektórych wprowadzić zależności w takim trójkącie.
Naprzeciwko najmniejszego kąta, czyli tego o mierze 30o leży bok najkrótszy, czyli a.
Naprzeciwko kąta o średniej mierze, czyli tego, którego miara wynosi 60o leży bok o średniej długości i jest to .
Naprzeciwko kąta największego, czyli kąta prostego, mającego miarę leży najdłuższy z boków, a jego długość wynosi .
Narysujmy taki trójkąt i przedstawmy te zależności na rysunku, żebyśmy mogli to lepiej zrozumieć.

Korzystając z tego rysunku obliczmy tangens kąta 30 stopni.
Stosunek długości przyprostokątnej leżącej naprzeciwko do długości przyprostokątnej stykającej się z tym kątem. Więc:

Możemy skrócić literę „a”.

Możemy również usunąć niewymierność z mianownika powstałego ułamka.
Mnożymy razy ułamek, którego licznik i mianownik jest równy i wynosi tyle samo ile mianownik naszego ułamka z, którego chcemy usunąć niewymierność.

Zadanie 1.
Oblicz ile wynosi długość „r”. Następnie podaj długość „c’.

Mamy zaznaczony kąt 30 stopni.
Naszym zadaniem jest wyznaczenie odcinka r.
Możemy skorzystać tutaj z funkcji trygonometrycznej, którą jest tangens.

Wyżej obliczyliśmy, że tangens 30 stopni ma wartość .
Możemy zatem podstawić do wzoru.

Korzystając z proporcji wymnóżmy na krzyż.

Obie strony równania podzielmy przez .

Pozbądźmy się niewymierności z mianownika.



Żeby obliczyć długość c możemy rozwiązać to zadanie na dwa sposoby.
Pierwszy z nich to użycie innej funkcji trygonometrycznej, natomiast drugi to skorzystanie z twierdzenia Pitagorasa i obliczenie długości przeciwprostokątnej.
Wykonajmy ten podpunkt na dwa sposoby.

I sposób.
Musimy skorzystać z funkcji trygonometrycznej w, której pod uwagę brana jest długość przeciwprostokątnej, czyli nasza niewiadoma. Korzystamy zatem z sinusa lub cosinusa.
Sinus to stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej.
Cosinus to stosunek długości przyprostokątnej przylegającej do kąta do długości przeciwprostokątnej.
Skorzystajmy z sinusa, a następnie z cosinusa żeby potwierdzić, że wszystko obliczyliśmy dobrze.

Z tabeli odczytujemy, że wartość sinusa 30 stopni to

Wykonujemy działania na krzyż.

Teraz sprawdźmy z wykorzystaniem cosinusa.

Wyżej obliczyliśmy, że
Z tabeli odczytujemy, że

Wymnóżmy na krzyż.

Podzielmy obie strony równania przez .

Zatem oraz .