Trójkąt ostrokątny

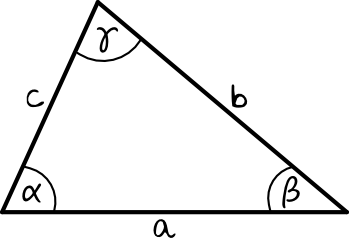
Trójkąt ostrokątny to trójkąt, który jak sama nazwa mówi, ma 3 kąty ostre. Co ważne, łączna suma tych kątów musi być równa 180 stopniom. W takim razie spróbujmy narysować kilka takich trójkątów.


Co ważne, w każdym trójkącie ostrokątnym miara kąta wewnętrznego musi być mniejsza od 90°.

Spróbujmy teraz odpowiedzieć na poniższe pytania.

Czy trójkąt ostrokątny może być różnoboczny?
Czy trójkąt ostrokątny może być równoramienny?
Czy trójkąt ostrokątny może być

1 . Weź do ręki kartkę, linijkę oraz kątomierz. Spróbuj narysować trójkąt, którego wszystkie kąty będą różnej miary (do 90°). Po narysowaniu takiego trójkąta, zmierz i zapisz długości poszczególnych boków. Zauważ, że każdy z boków jest innej długości. Oznacza to, że jeśli stworzysz trójkąt o miarach kątów np. 50°, 60° oraz 70°, to stworzysz trójkąt ostrokątny różnoboczny.



a, b oraz c są różne od siebie!!!

2 . Teraz narysuj trójkąt, którego miary kątów wewnętrznych również będą mniejsze od 90 stopni a większe od 0. Zwróć uwagę na to, aby miary kątów przy podstawie były takie same, a tym samym aby długości dwóch pozostałych boków były takie same.

Jak widzisz, bez problemu możemy stworzyć taki trójkąt. Może być to trójkąt, którego kąty wynoszą odpowiednio 50°, 50°, 80°.

Ramiona tego kąta są tej samej długości, oraz kąty przy podstawie mają tę samą miarę. Oznacza to, że możemy skonstruować trójkąt równoramienny ostrokątny.

3 . Na sam koniec zostawiłam Tobie do narysowania trójkąt, którego miary kątów wewnętrznych będą takie same. Tę miarę możemy obliczyć, dzieląc sumę kątów wewnętrznych trójkąta przez ich ilość, a więc: . W takim razie konstruujemy trójkąt o kątach 60°, 60°, 60°.

Spróbuj na początku narysować ten trójkąt tylko przy pomocy kątomierza. Gdy go narysujesz, zmierz za pomocą linijki długości boków trójkąta. Jak widzisz, każdy z boków trójkąta jest tej samej długości. Oznacza to, że trójkąt, którego kąty wewnętrze wynoszą odpowiednio 60°, 60°, 60° jest trójkątem równobocznym ostrokątnym.

Ten trójkąt jest takim szczególnym przypadkiem wszystkich trójkątów. Z tego powodu, mamy kilka wzorów, które pozwalają nam na łatwiejsze obliczenia podczas wykonywania zadań z tego zagadnienia.

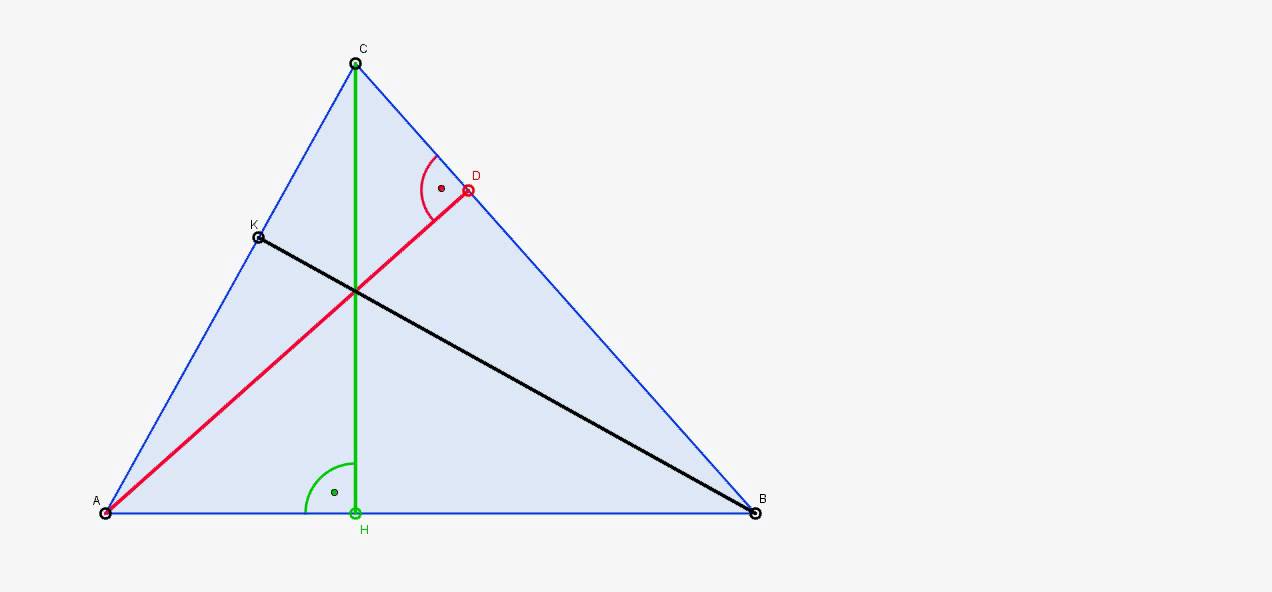
Zacznijmy od wysokości. Każdy trójkąt ma 3 wysokości. W każdym trójkącie ostrokątnym przecięcie tych trzech wysokości następuje wewnątrz tego trójkąta. Punkt ten jest nazywany ortocentrum trójkąta. Zazwyczaj jest on oznaczany jako „H”.



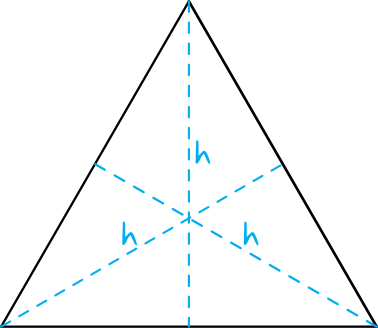
Powyżej masz pokazane trójkąty różnoboczne. Spójrz teraz na grafiki poniżej.



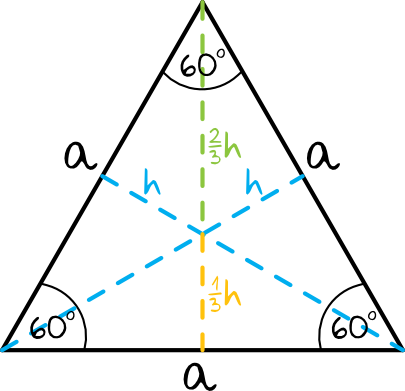
Zauważ, że wysokości w trójkącie równobocznym są tej samej długości, w przeciwieństwie do innych trójkątów ostrokątnych, gdzie te wysokości różnią się od siebie. Punkt, w którym wysokości się przecinają, dzieli każdą wysokość w stosunku 2 : 1, tym samym na dwa odcinki: oraz .

Aby obliczyć więc wysokość w takim trójkącie stosujemy wzór:

Pamiętamy, że aby obliczyć pole każdego trójkąta, w tym trójkąta ostrokątnego, możemy użyć wzoru: . Gdybyśmy do tego wzoru podstawili pod h wcześniej pokazany wzór, otrzymalibyśmy następujący wzór, który pozwala nam obliczyć pole powierzchni każdego trójkąta równobocznego. Ten wzór to: , gdzie a jest długością boku trójkąta.

zadanie 1
Oblicz miarę kąta alfa.

Rozwiązanie takiego zadania zaczynamy od przypomnienia sobie, że suma miar kątów w trójkącie to 180°. Na podstawie tego wnioskujemy, że:

Odpowiedź: Miara kąta alfa wynosi 70 stopni.

zadanie 2
Miara jednego z kątów w trójkącie równoramiennym wynosi 40°. Oblicz pozostałe miary kątów pamiętając o rozważeniu dwóch przypadków.

I przypadek

W pierwszym przypadku rozważmy, że kąt 40° znajduje się przy wierzchołku trójkąta. Pamiętamy, że kąty przy podstawie mają tę samą miarę, dlatego też bez problemu obliczymy te miary.

Odpowiedź: Miary kątów przy podstawie wynoszą po 70°. Tym oto sposobem otrzymaliśmy trójkąt równoramienny ostrokątny.

II przypadek

Autor zadania mógł jeszcze założyć, że ten kąt 40 stopni jest kątem przy podstawie. W takim razie naszą niewiadomą jest kąt przy wierzchołku trójkąta.

Odpowiedź: W drugim przypadku kąt wynosi 100°. Powstaje wtedy trójkąt równoramienny rozwartokątny.

Na sam koniec powiemy sobie jeszcze o środku ciężkości trójkąta. On każdą środkową, a więc prostą poprowadzoną z środka boku do naprzeciwległego wierzchołka trójkąta, dzieli w stosunku 2 : 1.

zadanie 3
Spróbuj obliczyć wysokość tego trójkąta równobocznego wiedząc, że ortocentrum trójkąta jest odległe o 3cm od podstawy tego trójkąta.

W związku z tym, że środkowe oraz wysokości w trójkącie równobocznym się pokrywają, mamy o wiele łatwiejszą sprawę do rozwiązania. Odległość zaznaczona jako x jest w takim razie 2 razy większa od 3cm, ponieważ ortocentrum trójkąta dzieli środkowe trójkąta w stosunku 2 : 1.

W takim razie wysokość to:

Odpowiedź: Wysokość tego trójkąta to 9cm.