Trygonometria

Zacznijmy od przedstawienia funkcji trygonometrycznych.
Funkcje trygonometryczne liczmy z kątów. Wyróżniamy ich 4.
Jest to: sinus, cosinus, tangens i cotangens.
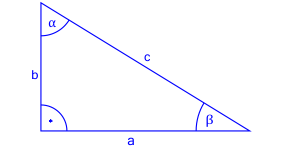
Zacznijmy od definicji tych funkcji i od ich zachowania w trójkącie prostokątnym.
Sinus to stosunek długości przyprostokątnej leżącej naprzeciwko kąta z, którego liczymy sinus do długości przeciwprostokątnej. (sin)
Cosinus to stosunek długości przyprostokątnej leżącej przy kącie (przylegającej do kąta) z, którego liczymy cosinus do długości przeciwprostokątnej. (cos)
Tangens to stosunek długości przyprostokątnej leżącej naprzeciwko kąta z, którego liczmy tangens do długości przyprostokątnej leżącej przy kącie (przylegającej do kąta). (tg)
Cotangens to odwrotność tangensa. Jest to stosunek przyprostokątnej leżącej przy kącie (przylegającej do kąta) do długości przyprostokątnej leżącej naprzeciwko tego kąta. (ctg)
Podajmy wartości funkcji trygonometrycznych kątów w trójkącie poniżej.





Jak możemy zauważyć pojawiły nam się pewne zależności:




Wiemy, że suma miar kątów w trójkącie wynosi 180 stopni. W naszym przypadku:


Wyznaczmy z tego równania jeden kąt. Niech będzie to

W taki sposób podstawiając do zależności, które ukazały nam się powyżej możemy przedstawić wzory redukcyjne.

Jak wiemy w matematyce znamy dwa trójkąty charakterystyczne. Pierwszy z nich to trójkąt o kątach 30, 60, 90 stopni. Drugi z nich natomiast to trójkąt w, którym kąty mają miary 45,45,90 stopni.
Wartości funkcji trygonometrycznych kątów 30,60 i 45 stopni dość często pojawiają się w zadaniach, dlatego ich wartości łatwiej nauczyć się na pamięć.

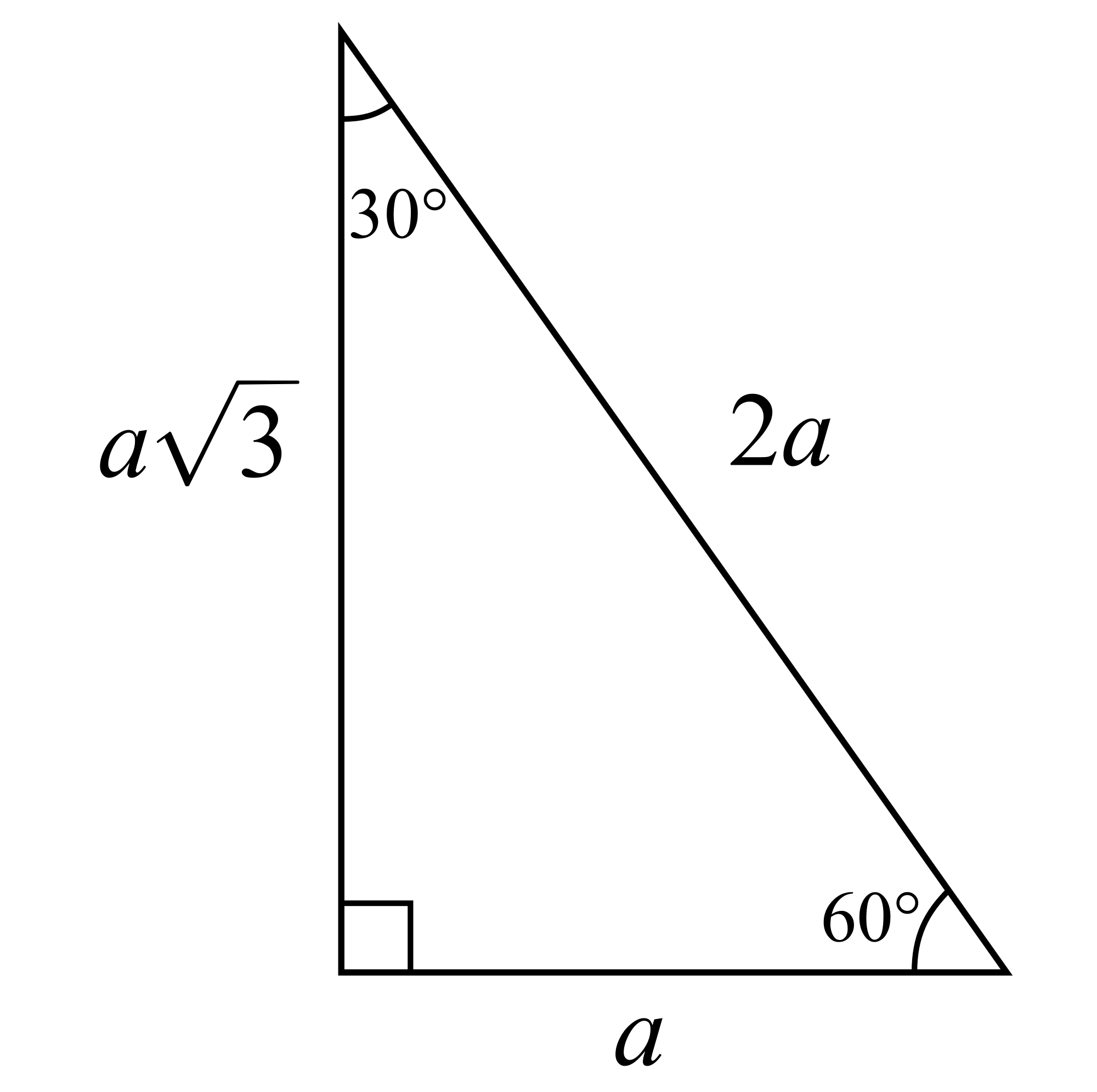
Zacznijmy od trójkąta 30,60,90.
Przypomnijmy zależności między bokami w takim trójkącie.
Naprzeciwko najmniejszego kąta, czyli 30 stopni leży najkrótszy bok, czyli „a”.
Naprzeciwko kąta o średniej mierze, czyli 60 stopni leży bok średniej długości, czyli „„.
Naprzeciwko największego kąta, czyli kąta prostego (90 stopni) leży najdłuższy bok- „2a”.
Przedstawmy te zależności na rysunku i obliczmy wartości funkcji trygonometrycznych kątów 30 i 60 stopni.

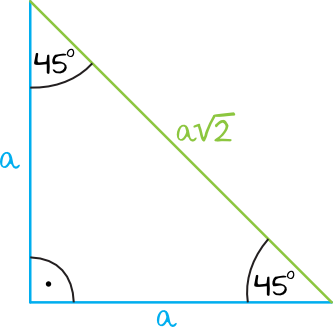
Przejdźmy teraz do trójkąta 45,45,90.
Przypomnijmy również zależności między bokami w takich trójkątach.
Naprzeciwko obydwu kątów o mierze 45 stopni leży ten sam bok- „a”.
Naprzeciwko kąta prostego, czyli o mierze 90 stopni leży dłuższy bok- „„
Przedstawmy teraz te zależności na rysunku i obliczmy wartości funkcji trygonometrycznych dla kąta o mierze 45 stopni.

Wartości trygonometryczne kątów 30,60,45 pojawiają się bardzo często w zadaniach z trygonometrii. Ich znajomość na pamięć przyspiesza rozwiązywanie zadań, ponieważ nie musimy ich od nowa liczyć, czy szukać w tabelce.
Żeby ułatwić naukę powstała tabelka, którą polecam Wam się nauczyć.

Obliczyliśmy wartości funkcji trygonometrycznych dla kątów charakterystycznych. Przejdźmy teraz do przećwiczenia podawania wartości trygonometrycznych dla innych kątów.
Zadanie 1.
Oblicz wartości trygonometryczne kąta zaznaczonego na poniższym rysunku.


Możemy skrócić przez 4.

Przejdźmy teraz do cosinusa.

Również skróćmy przez 4.

Następnie przejdźmy do tangensa.


Cotangens to odwrotność tangensa zatem:

Możemy usunąć niewymierność z mianownika.

Wartości funkcji trygonometrycznych mogą mieć wartości dodatnie, ale również ujemne. Skąd wiedzieć kiedy jaki dać znak? Został do tego stworzony specjalny wierszyk, rymowanka. Żeby jednak w pełni go rozumieć musimy przypomnieć podział układu współrzędnych na ćwiartki.

Każda ćwiartka mieści w sobie 90 stopni miar kąta.
Zatem:
W pierwszej ćwiartce są kąty o mierze od 0 do 90 stopni.
W drugiej ćwiartce są kąty o mierze od 90 do 180 stopni.
W trzeciej ćwiartce są kąty o mierze od 180 do 270 stopni.
W czwartej ćwiartce natomiast analogicznie do pozostałych znajdują się kąty o mierze od 270 do 360 stopni.
Przedstawmy teraz wierszyk dzięki któremu będziemy wiedzieć kiedy wartości trygonometryczne są dodatnie, a kiedy ujemne.
W pierwszej ćwiartce wszystkie są dodatnie,
W drugiej tylko sinus,
W trzeciej tangens i cotangens,
A w czwartej cosinus.
Zatem:
Dla kątów od 0 do 90 stopni wszystkie funkcje trygonometryczne mają dodatnie wartości.
Dla kątów od 90 do 180 stopni dodatni jest tylko sinus, reszta jest ujemna.
Dla kątów od 180 do 270 stopni dodatni jest tangens i jego odwrotność, czyli cotangens, natomiast sinus i cosinus są ujemne.
Dla kątów od 270 do 360 stopni dodatni jest tylko cosinus, natomiast pozostałe funkcje trygonometryczne przyjmują ujemne wartości.

Znając wartość jednej funkcji trygonometrycznej możemy obliczyć wartości innych funkcji trygonometrycznych.
Mając podany sinus lub cosinus korzystamy z tzw. „jedynki trygonometrycznej”.

Mając podany sinus i cosinus kąta możemy obliczyć tangens i cotangens tego kąta.

Skoro cotangens to odwrotność tangensa to:

Zadanie 1.
Wyznacz wartości pozostałych funkcji trygonometrycznych dla kąta ostrego , jeżeli wiesz, że:
a)
b)
c)
d)

Kluczowe w treści naszego zadania jest to, że kąt jest ostry. To oznacza, że każda wartość funkcji trygonometrycznych jest dodatnia.
Zacznijmy od podpunktu a.
Mamy podany sinus kąta. Korzystając z jedynki trygonometrycznej obliczmy cosinus tego kąta.






lub
Kąt jest ostry, więc cosinus jest dodatni.

Znamy już sinus i cosinus kąta możemy więc obliczyć tangens i cotangens.




Cotangens to odwrotność tangensa zatem:

Przejdźmy do podpunktu b.
Mamy podany cosinus kąta (gdy mamy podany sinus lub cosinus kąta ZAWSZE korzystamy z jedynki trygonometrycznej żeby obliczyć wartość innej funkcji trygonometrycznej)







lub
Kąt jest ostry, więc sinus tego kąta ma wartość dodatnią.

Znamy już sinus i cosinus tego kąta, więc korzystając ze wzoru na tangens obliczmy jego wartość.




Cotangens to odwrotność tangensa więc jest on równy:

Przejdźmy do podpunktu c.
Tutaj sytuacja jest trochę inna. Mamy podany tangens. Nie jest to ani sinus, ani cosinus, więc nie możemy skorzystać z jedynki trygonometrycznej.
Wykorzystajmy fakt, że .
Z treści zadania wiemy, że . Już na wstępie możemy podać cotangens, bo jest to odwrotność tangensa, czyli .
Podstawmy do powyższego wzoru na tangens wartość, że jest to

Skorzystajmy z proporcji i pomnóżmy na krzyż:


Teraz, gdy wyznaczyliśmy już ile wynosi cosinus możemy skorzystać z jedynki trygonometrycznej.

Podstawmy teraz w miejsce cosinus=4sinus




lub
Odrzucamy drugą opcję, bo kąt jest ostry (sinus, jak i inne funkcje trygonometryczne są dodatnie)

Pozbądźmy się niewymierności z mianownika. Mnożymy razy ułamek, który w mianowniku i liczniku ma mianownik naszego wyjściowego ułamka.


Znamy już sinus. Wcześniej natomiast wyznaczyliśmy, że .
Podstawmy więc wartość sinusa, którą wyliczyliśmy z jedynki trygonometrycznej.


Mamy już wyznaczone wartości wszystkich funkcji trygonometrycznych w tym podpunkcie.

Został nam podpunkt d.
Rozwiązujemy go analogicznie do podpunktu c.

Możemy podać cotangens.


W podpunkcie c korzystaliśmy z podstawienia do wzoru na tangens.
W tym przypadku również możemy tak zrobić, jednak chcę Wam pokazać, że można to też rozwiązać korzystając z wzoru na cotangens.
Skoro , to odwrotność tangensa, czyli cotangens wyraża się wzorem: .
Podstawmy zatem wartość cotangensa do tego wzoru:

W tym przypadku również mnożymy na krzyż.


Korzystając z „jedynki trygonometrycznej” obliczymy wartość cosinusa, a następnie sinusa.





lub
Cosinus jest dodatni, bo kąt jest ostry. Odrzucamy zatem drugą opcję.

Funkcje trygonometryczne możemy rozpatrywać i obliczać ich wartości także w układzie współrzędnych.
Kąt w układzie współrzędnych składa się z ramienia początkowego i ramienia końcowego.
Ramię początkowe to zazwyczaj oś OX (jej dodatnia część), natomiast położenie ramienia końcowego zmienia się w zależności od miary kąta.
Żeby obliczyć wartości funkcji trygonometrycznych potrzebujemy znać współrzędne punktu położonego na ramieniu końcowym.
Przyjmijmy, że taki punkt to

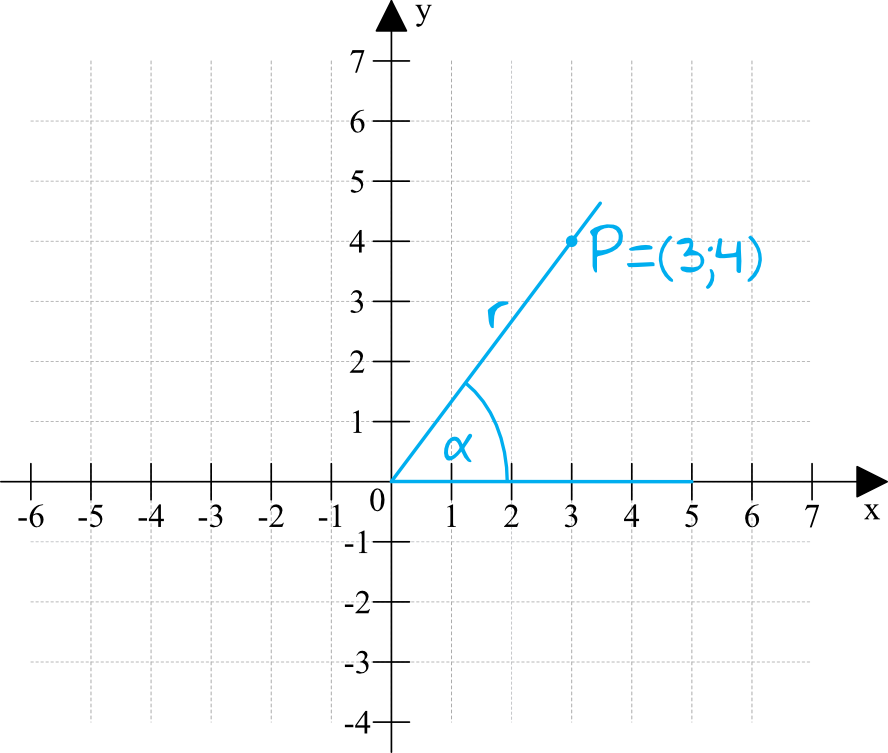
Przykład 1.
Wyznacz wartość wszystkich funkcji trygonometrycznych, którego jedno z ramion przechodzi przez punkt , a drugie pokrywa się z osią OX.
Przedstawmy sytuację na rysunku.

Zacznijmy od napisania czym jest „x”, czym jest „y”, a także obliczmy „r”.






Znamy już wszystko co potrzebujemy. Wystarczy tylko podstawić do wzorów.

W trygonometrii pojawiają się także wzory redukcyjne.
Przedstawmy je a następnie przećwiczmy ich zastosowanie.

Ćwiczenie 1
Podaj wartość:
a)
b)
c)

Podpunkt a.
Sinus kąta 150 stopni możemy rozpisać na sumę dwóch kątów (90+60)


Możemy również rozpisać ten kąt na drugi sposób.

Podpunkt b.
Cosinus kąta 135 stopni możemy rozpisać jako sumę kątów o mierze 90 i 45 stopni.


Drugi sposób na rozwiązanie tego zadania:

Podpunkt c.
Tangens 120 stopni możemy rozpisać jako sumę kątów o mierze 90 i 30 stopni.


Drugi sposób na rozwiązanie tego podpunktu:

Ćwiczenie 2
. Wyznacz miarę kąta .
W tym przypadku skorzystamy z wzoru:


Kąt ma miarę 63 stopni.

Trygonometria może nam się również przydać przy obliczaniu pól wybranych figur geometrycznych.
Przedstawmy wzory:
Dla trójkąta „a” i „b’ to długości boków trójkąta, natomiast kąt to kąt zawarty MIĘDZY TYMI RAMIONAMI („a” i „b”).
Dla rombu „a” to długość boków, natomiast to kąt między bokami.
Dla równoległoboku „a” i „b” to długości boków, natomiast to kąt między nimi.
Dla dowolnego (każdego) czworokąta „” oraz „” to długości przekątnych, natomiast to kąt zawarty między tymi przekątnymi.

Jak widzimy trygonometria ma szerokie zastosowanie i może nam się przydać w różnego typu zadaniach.
Mam nadzieję, że zrozumieliście dobrze ten szeroko pojęty temat, ponieważ w matematyce jest on niezwykle kluczowy i istotny. Polecam Wam nauczyć się wartości trygonometrycznych kątów charakterystycznych, ponieważ przyspieszy to rozwiązywanie zadań.