Trygonometria wzory

Jak wiesz, wyróżniamy cztery funkcje trygonometryczne: sinus, cosinus, tangens oraz cotangens. Te funkcje odpowiednio wyrażają stosunek długości danych boków w trójkącie prostokątnym.

Funkcje trygonometryczne wynoszą odpowiednio:

Zauważ, że sinus kąta alfa odpowiada cosinusowi kąta beta oraz na odwrót, a więc cosinus alfa odpowiada sinusowi beta. Tak samo jest z tangensem kąta alfa, który odpowiada cotangensowi kąta beta i na odwrót.

Jednym z najważniejszych wzorów, pozwalający nam obliczać wiele zadań związanych z trygonometrią, to tak zwana JEDYNKA TRYGONOMETRYCZNA. Przedstawia się ona następująco:

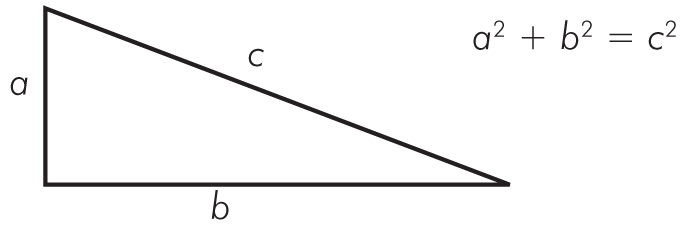
Spróbujmy wyprowadzić ten wzór bazując na poniższym trójkącie.

| :

Innymi ważnymi wzorami są wzory związane z tangensem i cotangensem.

Spróbujmy wyprowadzić ten wzór bazując na powyższym trójkącie.

Spróbujmy wyprowadzić ten wzór bazując na powyższym trójkącie.

Spróbujmy wyprowadzić ten wzór bazując na powyższym trójkącie.

Powyżej pokazane dowody to dowody słuszności twierdzeń!

Ponadto pamiętajmy, że:

W takim razie przejdźmy do rozwiązywania zadań.

zadanie 1
W pewnym trójkącie prostokątnym został zaznaczony kąt ostry alfa. Cosinus tego kąta wynosi . Podaj wartości pozostałych funkcji trygonometrycznych.

I sposób rozwiązania zadania

Rozwiązanie takiego zadania zaczynamy od odczytania długości przyprostokątnej przy kącie i przeciwprostokątnej.


b = 12
c = 13

Z twierdzenia Pitagorasa obliczamy długość boku a, a więc przyprostokątnej naprzeciw kąta.
a > 0

Następnie znając funkcje trygonometryczne wyznaczamy je:

II sposób rozwiązania zadania

W drugim sposobie rozwiązania tego zadania możemy zastosować jedynkę trygonometryczną. Poprzez podstawienie wiadomej nam funkcji trygonometrycznej możemy bez problemu obliczyć tego kąta. Następnie znając stosunek sinusa i cosinusa możemy obliczyć tangens oraz jego odwrotność, a więc cotangens.

Takim oto sposobem rozwiązaliśmy zadanie na dwa sposoby. Warto każde zadanie rozwiązywać na te właśnie dwa sposoby, a więc z twierdzenia Pitagorasa oraz ze wzorów trygonometrycznych.

zadanie 1
Oblicz wartość wyrażenia wiedząc, że

I sposób rozwiązania zadania

Wiemy, że —> z tego wynika, że
Zacznijmy od użycia jedynki trygonometrycznej i wyznaczmy, jaka zależność jest między sinusem a cosinusem.

Otrzymany wynik podstawiamy do naszego wyrażenia:

II sposób rozwiązania zadania

Jak widzisz, na początku sprowadziliśmy wartości w liczniku i mianowniku do wspólnego ułamka. Dzięki temu, że wiemy, że stosunek sinusa kąta alfa do cosinusa kąta alfa to tangens tego kąta, udało nam się w wiele miejsc podstawić wartość naszego tangensa. Następnie po prostu upraszczaliśmy równanie po to, aby otrzymać końcowy wynik.

III sposób rozwiązania zadania

Z twierdzenia Pitagorasa możemy obliczyć długości poszczególnych boków. Następnie bez problemu możemy podstawić te wartości, aby otrzymać wartości danych funkcji trygonometrycznych. Na podstawie tego bez problemu rozwiążemy te zadanie otrzymując oczywiście ten sam wynik.

Zadanie domowe:
Spróbuj rozwiązać te zadanie trzecim wyżej opisanym sposobem. Próbuj tak długo, aż dojdziesz do skutku. POWODZENIA!

Jak widzisz, powyżej zajmowaliśmy się kątami ostrymi, a więc od 0° do 90°. Oczywiście, mamy także duuuużo większe kąty. Z tego powodu wymyślono takie coś, jak wzory redukcyjne. One pozwalają nam z bardzo dużych kątów stworzyć odpowiednio mniejsze kąty, dla których obliczenie danych wartości trygonometrycznych nie będzie stanowiło dla nas problemu.

Narysujmy układ współrzędnych. W zależności od tego, w jakiej ćwiartce jesteśmy, dana funkcja trygonometryczna będzie miała znak dodatni albo ujemny.


Spójrz teraz na powyższą grafikę. Każda z ćwiartek, a w zasadzie jej znak mówi nam jaki znak przyjmuje ta funkcja w danej ćwiartce. To samo także widać na poniższym układzie współrzędnych.

Skoro już to wiemy, to przejdźmy do wzorów redukcyjnych. Jest ich dosyć sporo, lecz całe szczęście niektóre znajdują się one w tablicach maturalnych.
Spójrz jak wyglądają funkcje trygonometryczne dowolnego kąta. W zależności od położenia punktu P, kąty będą miały różne miary.

I ćwiartka

II ćwiartka

III ćwiartka

IV ćwiartka

Przykładowe zastosowanie wzorów redukcyjnych:

zadanie 1
Oblicz sinus 120 stopni.

I sposób rozwiązania (ten łatwiejszy)

Pamiętamy o tym, aby każdorazowo sprawdzić znak danej funkcji w danej ćwiartce.

II sposób rozwiązania (ten nieco trudniejszy –> przejście na co-funkcję)

Jak widzisz, oby dwa sposoby są poprawne. W pierwszym sposobie musieliśmy tylko pamiętać o sprawdzeniu znaku. W drugim sposobie zmieniliśmy funkcję sinus na cosinus i również pamiętaliśmy o znaku. Ja bardziej polecam pierwszy sposób, gdyż często można się po prostu pomylić przy zamianie tych funkcji.