Opracowanie:
Układ współrzędnych
Układ współrzędnych
Zacznijmy od przypomnienia czym jest układ współrzędnych, z czego się składa i jak się dzieli.
Układ współrzędnych to dwie prostopadłe do siebie proste prostopadłe. Prostopadłe tzn. przecinające się pod kątem prostym. Układ współrzędnych składa się z pionowej osi y, nazywanej także OY lub nazywana „oś rzędnych” oraz z poziomej osi x, nazywanej również OY lub nazywana „oś odciętych”.
Układ współrzędnych dzieli się na 4 części/4 ćwiartki, lecz nie są one ponumerowane od strony lewej do prawej tylko w trochę nietypowy sposób. Ten podział przedstawię Wam na rysunku, który zamieszczam pod spodem.
W układzie współrzędnych możemy zaznaczać różne punkty. Posiadają one dwie liczby, dwie współrzędne, które zapisywane są w nawiasie. P(x,y). Pierwsza współrzędna punktu to współrzędna „x”, czyli ta, którą odczytujemy z poziomej osi OX, natomiast druga współrzędna to współrzędna „y”, którą odczytujemy z pionowej osi OY.
Poćwiczmy zatem zapisywanie współrzędnych punktu.
Ćwiczenie 1.
Zapisz współrzędne punktów A,B i C. Określ w, której ćwiartce leżą poszczególne punkty.

Zacznijmy od punktu A.
Najpierw czytamy współrzędną z osi poziomej „x”.
Odczytujemy, że ta współrzędna dla punktu A będzie wynosiła -2.
Teraz druga współrzędna, współrzędna „y”, czyli ta czytana na osi pionowej.
Odczytujemy, że jest to 5.
Zatem punkt A(-2;5).
Punkt A leży w II ćwiartce.
Przejdźmy teraz do punktu B.
Pierwsza współrzędna, współrzędna „x”, czytana poziomo to 3.
Druga współrzędna, współrzędna „y”, którą odczytujemy z pionowej osi „y” to 2.
Zatem punkt B(3,2).
Punkt B leży w I ćwiartce.
Podajmy teraz punkt C.
Odczytujemy pierwszą współrzędną „x” z poziomej osi liczbowej „x”, jest to -1.
Druga współrzędna, współrzędna „y” odczytywana z osi pionowej to w przypadku naszego punktu współrzędna -2.
Zatem punkt C (-1;-2).
Punkt C leży w III ćwiartce.
Możemy zatem zauważyć, że:
W I ćwiartce leżą punkty, których obie współrzędne (współrzędna „x” oraz współrzędna „y”) są dodatnie.
W II ćwiartce leżą punkty, których pierwsza współrzędna („x”) jest ujemna, natomiast druga współrzędna („y”) jest dodatnia.
W III ćwiartce leżą punkty, których obie współrzędne ( współrzędna „x” oraz współrzędna „y”) są ujemne.
W IV ćwiartce leżą punkty, których pierwsza współrzędna („x”) jest dodatnia, natomiast druga współrzędna („y”) jest ujemna.
W układzie współrzędnych „jedna kreseczka” na osiach liczbowych może mieć różną wartość. Na jednej osi współrzędnych może wynosić 1, natomiast na innym może wynosić 5. Wszystko zależy od jednostki jaką przyjmiemy.
W układzie współrzędnych mogą być zaznaczane odcinki. Mogą one leżeć równolegle do osi, czyli po kratkach, ale mogą także leżeć na ukos.
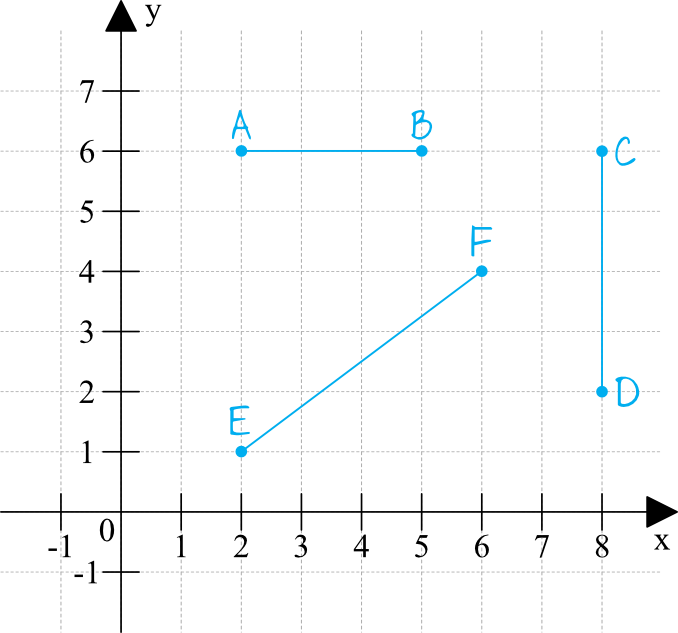
Zadanie 2.
Patrzymy na jednostki. Jedna kratka to 1.
Zatem, żeby obliczyć długość odcinka wystarczy policzyć ilość kratek które zajmuje. Jest to 3 kratki, zatem długość odcinka .
Tak samo postępujemy w przypadku odcinka .
Liczymy kratki. Jest ich 4, zatem odcinek .
Sytuacja trochę nam się komplikuje, gdy chcemy policzyć długość odcinka . Nie jest on położony równolegle do kratek więc nie możemy policzyć kratek, żeby podać jego długość.
W takiej sytuacji możemy działać na dwa sposoby.
Pierwszy z nich to dorysowanie przyprostokątnych żeby stworzyć trójkąt prostokątny i skorzystać z Twierdzenia Pitagorasa. Natomiast drugi sposób to skorzystanie ze wzoru na długość odcinka.
Pokażę Wam jak obliczyć długość odcinka na dwa sposoby.
Zacznijmy od sposobu 1 w, którym skorzystamy z Twierdzenia Pitagorasa.
Zacznijmy od tego czym jest to twierdzenie.
Twierdzenie Pitagorasa stosujemy w trójkącie prostokątnym. Mówi ono, że stosunek sumy kwadratów długości przyprostokątnych jest równy kwadratowi długości przeciwprostokątnej.
Wprowadźmy oznaczenia. Niech a, b to przyprostokątne, natomiast c to przeciwprostokątna.
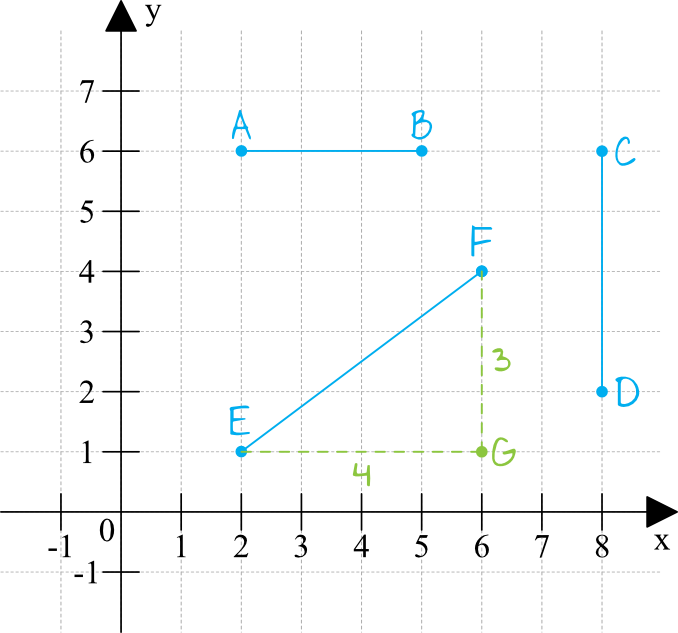
Dorysujmy zatem te przyprostokątne na naszym rysunku.
Przyprostokątna zajmuje 4 kratki, więc jej długość to 4, natomiast przyprostokątna zajmuje 3 kratki, więc jej długość to 3.
Zastosujmy Twierdzenie Pitagorasa.
lub
Długość odcinka nie może być ujemna, więc długość odcinka to 5.
Drugi sposób.
Wykorzystujemy wzór na obliczanie długości odcinka.
Skąd wziąć ?
Są to współrzędne punktów, które wyznaczają nam odcinek. W naszym przypadku współrzędne punktu E oraz punktu F.
Odczytajmy zatem jakie współrzędne mają te punkty.
Zacznijmy od E. Na osi poziomej ,czyli „x” ta liczba to 2, natomiast na „y”, czyli osi pionowej jest to 1.
Zatem punkt E x=2 y=1 E(2;1)
Podajmy teraz współrzędne punktu F. Odczytajmy najpierw na osi poziomej „x”. Jest to 6, natomiast na osi pionowej „y” jest to 4. Zatem punkt F x=6, y=4 F(6;4).
Podstawmy teraz do wzoru.
Nie ma znaczenia, który punkt oznaczymy jako 1, a który jako 2, ponieważ odcinek możemy podać jako lub i jest to to samo.
lub
lub
lub
lub
lub
Jak widzimy nie ma różnicy, który punkt oznaczymy jako 1, a który jako 2.
Długość odcinka .
Możemy także podać wzór na środek odcinka w układzie współrzędnych.
Ćwiczenie 1.
Podaj współrzędne środka odcinka o końcach w punktach oraz .
Jeżeli znamy współrzędne tych punktów możemy podstawić do wzoru.
Możemy również wykorzystać ten wzór, gdy znamy jeden z końców odcinka, a także jego środek, a chcemy podać drugi z końców tego odcinka
Ćwiczenie 2.
Środek odcinka ma współrzędne: . Oblicz współrzędne punktu , jeżeli wiesz, że punkt .
Korzystając z wzoru możemy zapisać, że:
Znamy współrzędne punktu B, więc możemy je podstawić.
Zatem punkt A ma współrzędne. .
W układzie współrzędnych możemy także rysować figury, których możemy obliczać pola, obwody, korzystając z znajomości obliczania długości odcinka.
Pokażmy to na przykładach.
Zadanie 3.
Oblicz pola oraz obwody figur zaznaczonych na rysunku poniżej.
Zacznijmy od trójkąta. Przypomnijmy wzór na pole trójkąta . W naszym przypadku a to odcinek , natomiast h musimy sobie dorysować i jest ona zaznaczona na zielono.
Podajmy długość odcinka |AB| oraz długość wysokości.
Podstawmy do wzoru na pole trójkąta.
Obwód to suma długości boków.
Znamy już długość odcinka , więc korzystając ze wzoru na długość odcinka obliczmy długość oraz .
Odczytajmy najpierw współrzędne punktów A, B oraz C.
Zacznijmy od obliczenia długości odcinka .
Teraz obliczmy długość odcinka .
Obwód=
Przejdźmy teraz do trapezu.
Przypomnijmy wzór na pole trapezu
Odcinek oznaczmy jako „a”, odcinek jako „b”. Musimy także dorysować wysokość „h”.
Podajmy długości tych odcinków.
Podstawmy te dane do wzoru:
Obliczmy teraz obwód. Mamy już odcinek oraz , teraz musimy obliczyć długości odcinków oraz .
Zapiszmy współrzędne tych punktów.
Zacznijmy od odcinka |ED|.
Teraz obliczmy długość odcinka |CF|.
Obwód:
Została nam jeszcze jedna figura, którą możemy podzielić na prostokąt i kwadrat.
Figura podzieliła nam się na prostokąt MNOR oraz kwadrat KLMP.
Pole figury KNORPL= Pole prostokąta MNOR + Pole kwadratu KLMP
Obliczmy pole prostokąta.
Przypomnijmy wzór
a- jeden bok
b- drugi bok
|ON| to jeden z boków
|MN| to drugi z boków
Podajmy ich długość
|ON|=5
|MN|=2
Obliczmy pole prostokąta MNOR.
Obliczmy teraz pole kwadratu KMPL.
Wzór:
a- bok
W kwadracie boki są jednakowej długości, więc obojętnie czy weźmiemy długość |PM|, czy |KM|, ponieważ są one takie same.
|PM|=|KM|=2
Mając już obliczone pole kwadratu i pole prostokąta możemy obliczyć pole całej figury.
Obliczmy teraz obwód tej figury:
Zbierzmy teraz informacje z dzisiejszego opracowania:
Układ współrzędnych składa się z osi pionowej „y” (nazywanej także OY lub osią rzędnych) oraz z poziomej osi „x” (nazwanej także OX lub osią odciętych)
Układ współrzędnych dzieli się na cztery ćwiartki.
W ćwiartce 1 obie współrzędne punktu ( współrzędna pozioma „x” oraz współrzędna pionowa „y”) są dodatnie.
W ćwiartce 2 pierwsza współrzędna punktu ( współrzędna pozioma „x”) jest ujemna, druga ( współrzędna pionowa „y”) jest dodatnia.
W ćwiartce 3 obie współrzędne punktu ( współrzędna pozioma „x” oraz współrzędna pionowa „y”) są ujemne.
W ćwiartce 4 pierwsza współrzędna punktu( współrzędna pozioma „x”) jest dodatnia, druga ( współrzędna pionowa „y”) jest ujemna.
Długość odcinka wyraża się wzorem:
We wzorze na długość odcinka nie ma znaczenia, który punkt wybierzemy jako pierwszy, a który jako drugi, ponieważ odcinek jest taki sam jak odcinek .
Środek odcinka wyraża się wzorem: .
Długość odcinka, który jest równoległy do kratek możemy obliczyć licząc kratki i sprawdzając jaką wartość ma jedna kratka.
Długość odcinka, który jest po skosie kratek możemy obliczyć korzystając z wzoru na długość odcinka lub dorysowując dwie przyprostokątne, żeby stworzyć trójkąt prostokątny.
Twierdzenie Pitagorasa to: .