Wartości trygonometryczne

Przypomnijmy definicje funkcji trygonometrycznych:
Sinus jest stosunkiem długości przyprostokątnej leżącej naprzeciwko kąta z, którego chcemy obliczyć sinus do długości przeciwprostokątnej.
Cosinus jest stosunkiem długości przyprostokątnej leżącej naprzeciwko kąta z, którego chcemy obliczyć cosinus do długości przeciwprostokątnej.
Tangens to stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przyprostokątnej leżącej przy kącie (przylega do kąta).
Cotangens to odwrotność tangensa. Cotangens to stosunek długości przyprostokątnej leżącej przy kącie (przylega do kąta) do długości przyprostokątnej leżącej naprzeciwko kąta.
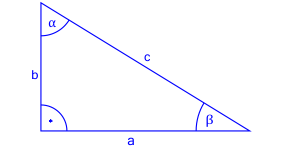
Pokażmy te zależności na rysunku:

Możemy zauważyć pewne zależności:

Jak wiemy układ współrzędnych dzieli się na 4 części.
Przypomnijmy ten podział:

Jeżeli chodzi o kąty to:
W pierwszej ćwiartce znajdują się kąty o mierze od 0 stopni do 90 stopni.
W drugiej ćwiartce znajdują się kąty o mierze od 90 stopni do 180 stopni.
W trzeciej ćwiartce znajdują się kąty o mierze od 180 stopni do 270 stopni.
W czwartej ćwiartce znajdują się kąty o mierze od 270 stopni do 360 stopni.
Jak możemy zauważyć w każdej ćwiartce znajduje się 90 stopni.
Wynika to z podziału kąta 360 stopni na cztery części, czyli tyle ile ćwiartek.
360:4=90
Jeżeli chodzi o wartości trygonometryczne to mamy nawet na ten temat specjalny wierszyk:

W pierwszej ćwiartce wszystkie są dodatnie,
W drugiej tylko sinus,
W trzeciej tangens i cotangens,
A w czwartej cosinus.

Zatem:
Kąty od 0 do 90- wszystkie wartości trygonometryczne są dodatnie.
Kąty od 90 do 180- sinus jest dodatni natomiast cosinus, tangens i cotangens są ujemne.
Kąty od 180 do 270- tangens i cotangens są dodatnie natomiast sinus i cosinus ujemne.
Kąty od 270 do 360- cosinus jest dodatni natomiast sinus, tangens i cotangens są ujemne.

Pokażmy zatem na zadaniach. Zacznijmy od trójkąta prostokątnego, czyli kąty ostre od 0-90.

Zadanie 1.
Oblicz wartości zaznaczonego kąta oraz drugiego kąta ostrego w tym trójkącie prostokątnym.

Drugi kąt nazwijmy
Zacznijmy od zaznaczonego na rysunku kąta .
Przypomnijmy definicje funkcji trygonometrycznych.
Sinus to stosunek przyprostokątnej leżącej naprzeciwko kąta do przeciwprostokątnej.
Cosinus to stosunek przyprostokątnej przylegającej do kąta do przeciwprostokątnej.
Tangens to stosunek przyprostokątnej naprzeciwko kąta do przyprostokątnej przylegającej do tego kąta.
Cotangens to odwrotność tangensa, czyli stosunek przyprostokątnej przylegającej do kąta do przyprostokątnej naprzeciwko kąta.




Obliczmy teraz wartości trygonometryczne drugiego kąta ostrego.

Zróbmy teraz zadanie z kątami powyżej 90 stopni.
Musimy wtedy korzystać z wzorów redukcyjnych.
Zadanie 2.
Oblicz wartość wyrażenia:
Zapiszmy zatem wzory redukcyjne:

Dla kąta

Dla kąta

Znając wzory redukcyjne możemy zapisać wartości poszczególnych funkcji trygonometrycznych.



Skoro już zredukowaliśmy wyrażenie zapiszmy je w prostszej postaci.

Korzystając z tabelki wartości, którą zamieszczę Wam pod spodem podstawimy wartości.


Obliczyliśmy wartość wyrażenia korzystając z wzorów redukcyjnych. Znak „-” przy cosinusie, tangensie i cotangensie wynika z wierszyka który pisaliśmy „w drugiej dodatni jest tylko sinus”…
Mam nadzieję, że zrozumieliście ten temat!