Wzór na wysokość trójkata

Obliczanie wysokości w trójkątach to rzecz, którą nauczysz się po przeczytaniu tego artykułu.

Spróbujmy najpierw wyprowadzić najbardziej ogólny wzór, pozwalający nam obliczyć wysokość w każdym trójkącie. Wzór ten wyprowadzimy z ogólnego wzoru na pole trójkąta. Przejdźmy do obliczeń (P, a, h muszą być większe od zera).



Ten wzór należy zapamiętać, gdyż jest to najbardziej ogólny wzór na wysokość trójkąta. Jednakże aby go zastosować, konieczna jest znajomość pola powierzchni figury oraz długości boku, na który została poprowadzona wysokość. Zazwyczaj ten bok jest podstawą.
Warto jednak wspomnieć, że nauka tego wzoru na pamięć nie jest konieczna. Myślę, że każdy z nas pamięta wzór na pole trójkąta. Znając go w każdej chwili bez problemu możemy wyznaczyć wzór na wysokość trójkąta. Przejdźmy teraz do bardziej szczegółowego spojrzenia na wysokości poszczególnych trójkątów.

Zacznijmy najpierw od najprostszego trójkąta, jakim jest trójkąt równoboczny. Ta figura ma kilka swoich bardzo ważnych własności. Przede wszystkim z racji tego, że jest ta figura trójkątem równobocznym, to kąty wewnętrzne odpowiednio wynoszą po 60°. Następnie możemy zauważyć, że jak każdy trójkąt ma on trzy wysokości. Co ważne, każda z tych wysokości jest tej samej długości.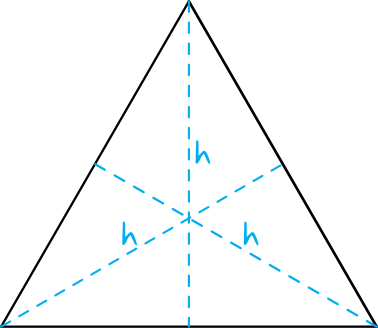

My jednak skupmy swoją uwagę na wysokości, która została poprowadzona z wierzchołka trójkąta.

Jak widzisz, wysokość dzieli ten trójkąt równoboczny na dwa trójkąty charakterystyczne, o miarach kątów 30°, 60°, 90°. Tym samym możemy sobie przypomnieć, że te zależności długości boków wyglądały o tak.

Stąd możemy wyprowadzić wzór, że dla każdego trójkąta równobocznego o boku a, wysokość wynosi:
W związku z tym wzorem, przydać nam się jeszcze może wzór na pole takiego trójkąta. Wzór ten to:

Tym samym jak widzisz, w każdym trójkącie 30°, 60°, 90° wysokość, którą stanowi bok, przy którym kąty mają miare 30° oraz 90°, to jest

Przejdźmy teraz do trójkątów równoramiennych. Te trójkąty ramiona mają tej samej długości, kąty przy podstawie są takie same. Podstawa będzie zatem innej długości oraz kąt przy wierzchołku będzie różnić się miarą od kątów przy podstawie. Jak się pewnie domyślasz, w tym trójkącie będzie również trzy wysokości. Z tą różnicą, że dwie będą tej samej długości. Ta poprowadzona w wierzchołka trójkąta będzie innej długości od pozostałych.

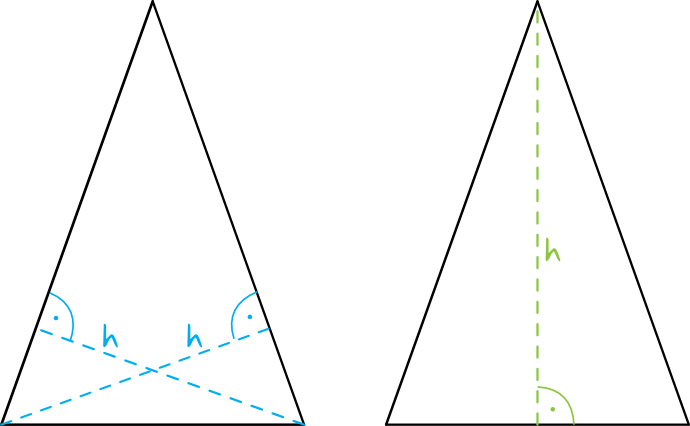
Jak więc policzyć wysokość tego trójkąta po lewej?

Najłatwiej wyznaczyć tę wysokość z twierdzenia Pitagorasa:

Skoro mówimy o trójkącie równoramiennym, to warto też wspomnieć o szczególnym przypadku trójkąta, który powstaje po narysowaniu przekątnej w kwadracie. Przekątna ta wyrażona jest wzorem . Tak więc powstaje nam trójkąt równoramienny o kątach 45°, 45°, 90°.

W tym trójkącie pierwszą wysokość będzie stanowić a, drugą wysokość będzie stanowić kolejny raz a. Trzecia wysokość to wysokość poprowadzona z kąta ostrego na przeciwprostokątną.

Tę wysokość również najłatwiej byłoby wyprowadzić z twierdzenia Pitagorasa:

Przed rozpoczęciem rozwiązywania zadań warto jeszcze wspomnieć o wzorze, który nie cieszy się dużą popularnością wśród młodzieży. Jednakże, często ułatwia obliczenia. Ten wzór będzie dotyczyć trójkątów prostokątnych. Co ważne, ten wzór działa tylko dla wysokości, która jest opuszczona z wierzchołka na przeciwprostokątną.

W takim wypadku po użyciu dwóch wzorów na pole trójkąta, a następnie podstawienia do tego twierdzenia Pitagorasa, a więc po wielu obliczeniach otrzymujemy wniosek, że

zadanie 1
Oblicz wysokość trójkąta prostokątnego, w którym opuszczona z wierzchołka wysokość podzieliła podstawę na dwa odcinki długości 4 oraz 12.

Rozwiązanie zaczynamy od napisania danych oraz narysowania rysunku pomocniczego. Następnie wszystko podstawiamy do wzoru i otrzymujemy wynik.

Odpowiedź: Wysokość wynosi

zadanie 2
Oblicz długość wysokości trójkąta o podstawie 2cm oraz polu

Odpowiedź: Wysokość trójkąta to 8cm.